Chapter 5: First-Order Inference

Tableau-Methode für die Prädikatenlogik 1. Stufe

Wiederholung: Propositional Inference

Da die Aussagenlogik entscheidbar ist, ist es möglich einen Theorem Prover zu bauen, der für jede Formel entscheidet, ob sie gültig ist.

Ein solcher Beweiser ist jedoch nie effizient, da das Problem NP-Vollständig ist.

Beispiel: Schubfachprinzip

/*------------------------------------------------------------------------
     Pigeonehole principle with 3 pigeons and 2 pigeonholes. 
------------------------------------------------------------------------*/

formula(imp(and(and(or(p11,p12),or(p21,p22)),or(p31,p32)),
            or(or(or(or(or(and(p11,p21),and(p11,p31)),and(p21,p31)),
               and(p12,p22)),and(p12,p32)),and(p22,p32))), 'Theorem').

pij Taube i in Loch j
$A \rightarrow B$; A: jede Taube ist in einem Loch; B: in einem Loch sitzt mehr als eine Taube.

Tableaumethode für die Prädikatenlogik („menschliche“ Version)

Tableau-Methode für die Prädikatenlogik (algorithmisch)

Unifikation und Substitution

Grundidee:

Durch die universelle Regeln werden nicht beliebige Terme sondern freie Variablen in das Tableau eingeführt.
Am Ende sollen diese Variablen durch Terme so ersetzt werden, dass Äste des Tableaus geschlossen werden können.
Die Ersetzung nennt man Substitution.
Ziel ist es eine Subsitution zu finden, die zwei Ausdrücke gleich macht, das nennt man Unifikation.

Wenn $\sigma= \{x/a,y/g(b)\}$ was ist dann

$g(x)\sigma$?
$y\sigma$?
$b\sigma$?
$z\sigma$?

$\sigma_x$ ist die folgende Substitution:
$x\sigma_x = x$ und $v\sigma_x=v\sigma$ für alle $v\neq x$.

Wenn $\sigma= \{x/a,y/g(b)\}$ was ist dann

$[\forall y \exists x ((P(y) \wedge Q(x,y) \rightarrow P(x))]\sigma$?

Frage: Die „more general than“-Relation auf Substitutionen ist reflexiv und transistiv, warum?

disagreement pair: w and k(u,v)

Beispiel: b und c bilden ein „disagreement pair“, da weder b noch c eine Variable ist, sind die beiden Terme nicht unifizierbar

Beispiel: y und f(a,y,b) bilden ein disagreement pair. Da y eine Variable ist, die in f(a,y,b) vorkommt, sind die beiden Terme nicht unifizierbar.

Definition: Ein “disagreement pair” $(d_1, d_2)$ heißt “simple”, genau dann wenn der Ausdruck $d_1$ oder $d_2$ (oder beide) eine Variable ist, die nicht in dem anderen Ausdruck vorkommt.

Algorithmus zur Term-Unification:

input terms t1 and t2
let s:={}
while t1s != t2s
    choose a disagreement pair (d1,d2) for t1s, t2s
    if (d1,d2) is not simple then
        write t1 and t2 are not unifiable and HALT
    else
        let s := s U r, where r is the relevant repair
    endif
endwhile

Der Algorithmus terminiert immer und wenn er eine Substitution ausgibt, gibt er eine idempotente Substitution $\sigma \sigma = \sigma$ aus, die zum mgu von t1 und t2 führt.

Vorsicht, gewöhnliche Prolog-Unifikation verzichtet auf den occurs-check. Es gibt aber das eingebaute unify_with_occurs_check/2-Prädikat, das eine Unifikation mit occurs-check durchführt.

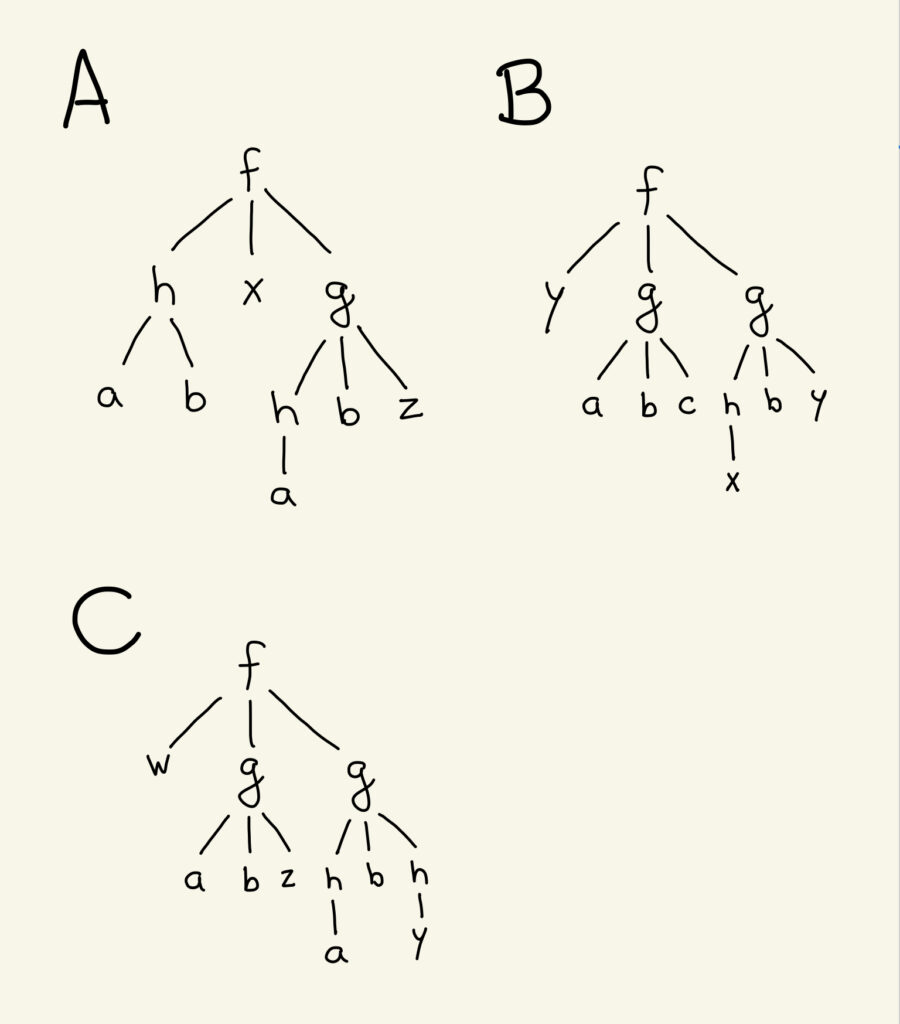
**Aufgabe:** Welche der drei Terme A, B und C lassen sich unifizieren? Was ist der mgu?

Simultane Unifikation

Mithilfe von Unifikation möchten wir versuchen Tableaux Branches zu schließen
Wir schauen uns dafür die Branches an, die Paare aus atmoren Formeln beinhalten:
$T(R( \tau_1, …, \tau_n))$ und $F(R(\tau’_1 , … , \tau’_n ))$.
Wenn wir eine Substitution $\sigma$ finden können, die $\tau_1$ identisch macht zu $\tau’_1$, und $…, \tau_n$ zu $\tau’_n$, dann erhalten wir durch die Anwendung von $\sigma$ einen Branch, der widersprüchliche Formeln enthält, was ein geschlossener Branch ist
Wir müssen also eine einzige Substitution finden, die gleichzeitig n Paare von Termen identisch macht.
Dies sieht schwieriger aus als eine gewöhnliche Substitution, ist es aber nicht.

Zum gleichzeitigen unifizieren von $\tau_1, …, \tau_n$ und $\tau’_1 , … , \tau’_n$ :

finde einen idempotenten mgu $\sigma_1$ für $\tau_1$ und $\tau’_1$
finde einen idempotenten mgu $\sigma_2$ für $\tau_2 \sigma_1$ und $\tau’_2 \sigma_1$
finde einen idempotenten mgu $\sigma_3$ für $\tau_3 \sigma_1$ und $\tau’_3 \sigma_1$
Kurz: Kette die Lösungen zu jedem einzelnen Paar aneinander

Die so erhaltene Substitution $\sigma = \sigma_1 \sigma_2 … \sigma_n-1 \sigma_n$ ist ein simultanes mgu der n Begriffspaare.

Free Variable Tableaux

Beispiel für die Wichtigkeit der Skolem-Terme als Funktionsterme über den freien Variablen:

Die folgende Formel ist erfüllbar:

$$ \exists y(\neg R(x,y)\wedge R(x,x))$$

Was wäre ein Modell, das die Erfüllbarkeit zeigt?

Zur Erinnerung: Wenn man ein Tableau mit einer erfüllbaren Formel eröffnet, dann kann das Tableau nicht geschlossen werden.

Die Formel enthält die freie Variable $x$, daher muss die existenzgebundene Variable $y$ durch den Skolemterm $s(y)$ substituiert werden:
$$ \neg R(x,s(x))\wedge R(x,x)$$

Nur so wird sichergestellt, dass $x$ und $y$ nicht unifiziert werden können.

Hätte man $x$ durch eine einfache Skolemkonstante $s$ substituiert, dann könnte man später $y$ ebenfalls durch $s$ substituieren und käme dann zur nicht erfüllbaren Formel
$$ \neg R(s,s)\wedge R(s,s).$$

Beispiel eines Tableau-Beweises:

Implementierung der Tableaumethode

FOL Resolution

FOL Resolution (Grundidee)

Umwandlung der Formel in CNF (Clause Normal Form)

Umwandlung in NNF (Negation Normal Form), d.h. es erscheinen nur noch die Operatoren ∧ und ∨, die Quantoren, Literale und Klammern.
Eliminiere die Existenzquantoren durch Skolemisierung.
Lösche alle Allquantoren.
Wandle die resultierende quantorenfreie Formel in (set) conjunctive normal form um.

Hinweise

Bei der Umwandlung in NNF wenden wir folgende Regeln an, um die Negation nach innen zu schieben: $\neg \forall x P(x)$ wird zu $\exists x \neg P(x)$ und $\neg \exists x P(x)$ wird zu $\forall x \neg P(x)$.
Bei der Skolemisierung müssen wir einen Fall besonders betrachten: Existenzquantoren im Skopus von Allquantoren.

Ist ein Existenzquantor im Skopus eines Allquantors, setzen wir statt Skolemkonstanten komplexe Skolemterme (sprich Skolemfunktionen) ein. Bsp.: $\forall x \exists y R(x,y)$ wird skolemisiert zu $\forall x R(x,s(x))$. Der komplexe Skolemterm drückt die Abhängigkeit der existenzgebundenen Variablen von der allgebundenen aus. $s(x)$ kann also als Funktion betrachtet werden, die jedem Element des Models ein Element zuordnet, zu dem es in der Relation $R$ steht.

Beispiel: Bringe $(\forall x B(x) \wedge \exists y A(y,x)) \rightarrow \exists z \forall x \exists y C(x,z) \vee B(z,y)$ in setCNF

Wir sorgen also per $\alpha$-Konversion zunächst dafür, dass die Variablenmengen in den beiden Klauseln disjunkt sind.

Non-redundant Factors:

Zur Erinnerung in PL Resolution haben wir mit Mengen-Klauseln gearbeitet $[[p],[\neg p]]$ statt $[[p,p],[\neg p,\neg p]]$.
In POL-Resolution müssen wir mit nichtredundanten Faktoren arbeiten.
Zwei Formeln in einer Klausel sind redundant, wenn sie unifizierbar sind.

Beispiel: Seien $w,x,y,z$ Variablen und $a,b,c$ Konstanten. Die Klausel $[P(a),P(x),R(y,b),R(z,x),\neg Q(w),\neg Q(f(z))]$ kann reduziert werden zu

$[P(a),R(y,b),R(z,a),\neg Q(f(z))]$ (unifiziere $P(a)$ und $P(x)$ und anschließend $\neg Q(w)$ und $\neg Q(f(z))$).
oder zu $[P(a),P(b),R(y,b),\neg Q(f(y))]$ (unifiziere $R(y,b)$ und $R(z,x)$ und anschließend $\neg Q(w)$ und $\neg Q(f(y))$).

Wir müssen jeweils alle nichtredundanten Faktoren einer Klausel behalten, da wir sonst möglicherweise keinen Beweis finden, obwohl es einen gäbe.

Implementing FOL Resolution

Bearbeiten Sie die Aufgaben 5.6.1 bis 5.6.3.

Theorem Provers and Model Builders

Zusammenfassung

Theorembeweiser ermöglichen es die Nichtkonsistenz einer Aussage in Bezug auf andere Aussagen nachzuweisen.
Model Builder ermöglichen es (partiell) die Konsistenz einer Aussage in Bezug auf andere Aussagen nachzuweisen.
Theorembeweiser ermöglichen es die Uninformativität einer Aussage in Bezug auf andere Aussagen nachzuweisen.
Model Builder ermöglichen es (partiell) die Informativität einer Aussage in Bezug auf andere Aussagen nachzuweisen.

Off-the-Shelf Theorem Provers

Die Resolutionsmethode ist sehr einfach, allerdings in der plumpen Form, in der wir sie implementiert haben auch sehr ineffizient.
Auch haben wir die Behandlung von Gleichheit bisher nicht implementiert. Man könnte sie theoretisch hinzufügen, indem man jedem Aufruf die Axiome des Gleichheitsprädikats hinzufügt:
- $\forall x (x=x)$
- $\forall x \forall y (x=y \rightarrow y=x)$
- $\forall x \forall y \forall z (x=y \wedge y=z \rightarrow x=z)$
Wenn man das macht, wird man feststellen, dass die Verarbeitung sehr langsam wird. Teste zum Beispiel die Inkonsistenz von „Mia does not snort“ in Bezug auf die Sätze „Every woman snorts“ und „Mia is a woman“.
Viele moderne Theorembeweiser beruhen auf der Resolutionsmethode. Sie verwenden aber wesentlich effizientere Methoden zur Verarbeitung von Gleichheit und implementieren diverse Strategien zur Wahl möglichst effektiver Resolutionsschritte.

Teste:

?- EQ = and(and(all(X,gleich(X,X)),all(X,forall(Y,imp(gleich(X,Y),gleich(Y,X))))),all(X,all(Y,all(Z,imp(and(gleich(X,Y),gleich(Y,Z)),gleich(X,Z)))))),
  Kontext = and(all(X,imp(woman(X),snort(X))),some(X,and(woman(X),gleich(mia,X)))),
  New = not(snort(mia)),
rprove(imp(and(EQ,Kontext),not(New))).

Im folgenden konzentrieren wir uns auf den Theorembeweiser Otter:

Folgt bitte den Anweisungen in How_to_Curt.html (link siehe Kurswebsite) bis einschließlich „Testen“.

Beispiel: $\forall x dance(x) \rightarrow \neg\exists x \neg dance(x)$

?- fol2vampire(imp(all(X,dance(X)),not(some(Y,not(dance(Y))))),user).

fof(

list_of_formulas,
conjecture,
( ( ! [A] : dance(A) ) => ~ ( ( ? [B] : ~ ( dance(B) ) ) ) )
).

?- fol2otter(imp(all(X,dance(X)),not(some(Y,not(dance(Y))))),user).

set(auto).
assign(max_seconds,30).
clear(print_proofs).
set(prolog_style_variables).
formula_list(usable).
((all A dance(A)) -> -((exists B -(dance(B))))).
end_of_list.

?- callTP(imp(all(X,dance(X)),not(some(Y,not(dance(Y))))),P,E).

Off-the-shelf Theorem Provers

Vampire (https://vprover.github.io)
Otter (http://www-unix.mcs.anl.gov/AR/otter/)
The E! Theorem Prover (https://wwwlehre.dhbw-stuttgart.de/~sschulz/E/E.html)

Off-the-Shelf Model Builder

Im folgenden fokussieren wir uns auf den Model Builder MACE.

Beispiel: $\forall x boxer(x)\rightarrow slow (x) \wedge boxer(butch) \wedge likes(mia,butch)$

?- fol2mace(and(all(X,imp(boxer(X),slow(X))),and(boxer(butch),likes(mia,butch))),user).

set(auto).
clear(print_proofs).
set(prolog_style_variables).
formula_list(usable).
((all A (boxer(A) -> slow(A))) & 
     (boxer(butch) & 
          likes(mia,butch))).
end_of_list.

callMB/4
callMB(Problem,DomainSize, Model, ModelBuilder).

?- callMB(and(all(X,imp(boxer(X),slow(X))),and(boxer(butch),likes(mia,butch))),5,Model,MB).


Model = D=[d1]
  f(1,boxer,[d1])
  f(1,slow,[d1])
  f(0,butch,d1)
  f(0,mia,d1)
  f(2,likes,[(d1,d1)])
,
MB = mace.