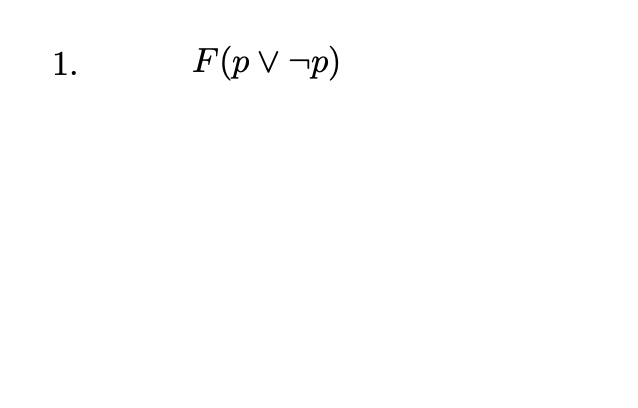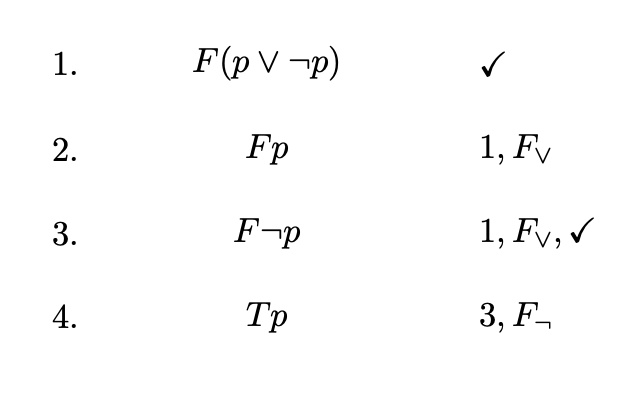Chapter 4: Propositional Inference

Wiederholung Kapitel 1

The Querying Task

Erfüllt ein Modell eine Aussage?

The Querying Task: Given a model $M$ and a first-order formula $\phi$ and a variable assignment, is $\phi$ satisfied in $M$ or not?

• Querying Task for first-order logic is decidable (Solution: Model Checker)

% satisfy/4
% statisfy(Formula,Model,Assignment,Polarity)

The Consistency Checking Task

Ist eine Aussage konsistent, sprich erfüllbar, sprich in wenigstens einem Modell erfüllt?

• consistency ≈ makes sense
• inconsistency ≈ does not make sense

A first-order formula is called satisfiable if it is satisfied in at least one model. A formula that is not satisfiable in any model is called unsatisfiable.

The Consistency Checking Task: Given a first-order formula $\phi$, is $\phi$ consistent (that is: satisfiable) or inconsistent (that is: unsatisfiable)?

• Consistency checking for first-order logic is undecidable

The Informativity Checking Task

Ist eine Aussage informativ, sprich nicht trivial, sprich nicht in jedem Modell erfüllt?

• informative = invalid
• uninformative (= trivial) = valid

A valid formula is a formula that is satisfied in all models (of the appropriate vocabulary) given any variable assignment. If $\phi$ is a valid formula we write $\vDash\phi$ . A formula that is not valid is called invalid $(\nvDash\phi$).

• Informativity checking for first-order logic is undecidable

Zusammenfassung

• Die Überprüfung auf Konsistenz und Informativität einer Aussage lässt sich jeweils auf die (Nicht-)Erfüllbarkeit der Aussage zurückführen:

* eine Aussage ist informativ, wenn es ein Modell gibt, in dem sie nicht erfüllt ist. 
* eine Aussage ist informativ, wenn ihre Negation erfüllbar ist. 
* eine Aussage ist konsistent, wenn sie erfüllbar ist.

• Die Erfüllbarkeit einer Aussage ist im Allgemeinen für die Prädikatenlogik unentscheidbar, für das Fragment ohne Quantifikatoren ist sie aber entscheidbar.
• $\psi$ ist inkonsistent in Bezug auf die Aussagen $\phi_1,\dots,\phi_n$, wenn
  $\phi_1,\dots,\phi_n\vDash \neg\psi$ gilt.
• $\psi$ ist uninformativ in Bezug auf die Aussagen $\phi_1,\dots,\phi_n$,
  wenn $\phi_1,\dots,\phi_n\models\psi$ gilt.
• $\phi_1,\dots,\phi_n\models\psi$ gilt, wenn $\phi_1 \wedge \dots\wedge\phi_n \rightarrow \psi$ eine gültige Aussage ist (also eine Aussage, die in allen Modellen gilt)
• $\phi_1,\dots,\phi_n\models\psi$ gilt, wenn $\phi_1\wedge\dots\wedge\phi_n\rightarrow\neg\psi$ eine unerfüllbare Aussage ist (also eine Aussage, die in keinem Modell gilt)

From Models to Proofs (BB: 4.1)

• Informativität und Konsistenz sind semantische Konzepte, die Aussagen über Modelle machen.
• Automatisch lassen sich Aussagen über alle Modelle nicht direkt überprüfen.
• Stattdessen verwenden wir einen beweistheoretischen Ansatz, der rein syntaktisch auf Formeln operiert, um die Gültigkeit einer Aussage zu beweisen.

Propositional Tableaus (BB: 4.2)

The Tableau Method

• Syntactic, but based on clear semantic intuitions.
• Finding a tableau proof does not depend on human insight.
• Can be adapted to many different logics.
• Tableau systems are more than just theorem provers: They can also be regarded as model building tools.

Proof by Refutation: Die Tableau-Methode ist eine Widerlegungsmethode. Statt zu zeigen, dass eine Formel $\phi$ gültig ist, zeigen wir, dass die negierte Formel $\neg\phi$ ungültig ist (also in keinem Modell erfüllbar).

Im Tableau: mit $F$ signierte Formeln werden als falsch behandlet, mit $T$ signierte Formeln werden als wahr behandelt. Also um zu zeigen, dass $\phi$ gilt, beginne mit $F\phi$

FRAGE: Warum verwenden wir nicht einfach Wahrheitstafeln?

Tableau rules

Examples

Beispiel 1:

Im folgenden soll die Gültigkeit von $\neg(q \wedge r) \rightarrow (\neg q \vee \neg r)$ überprüft werden:

❮ ❯

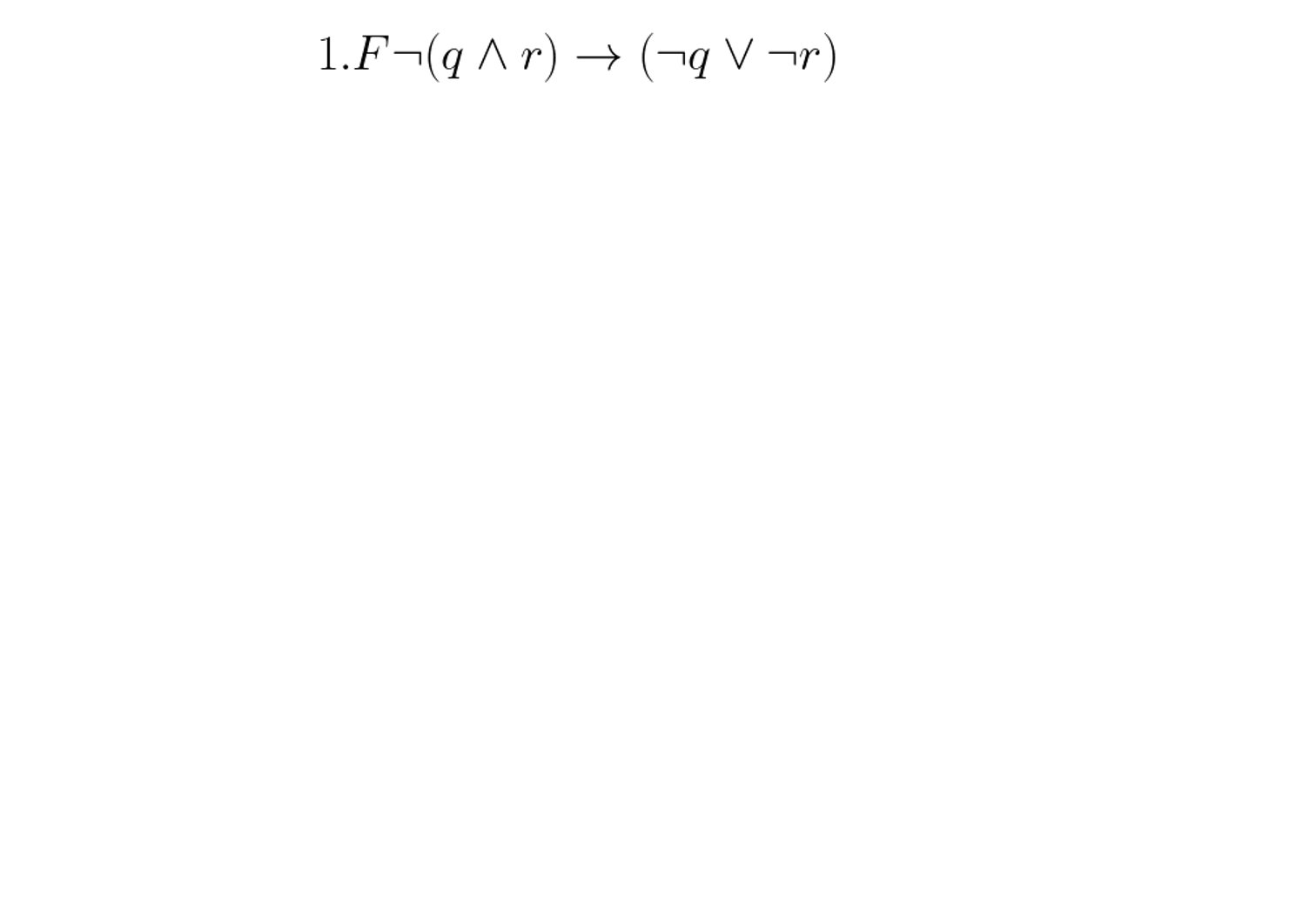
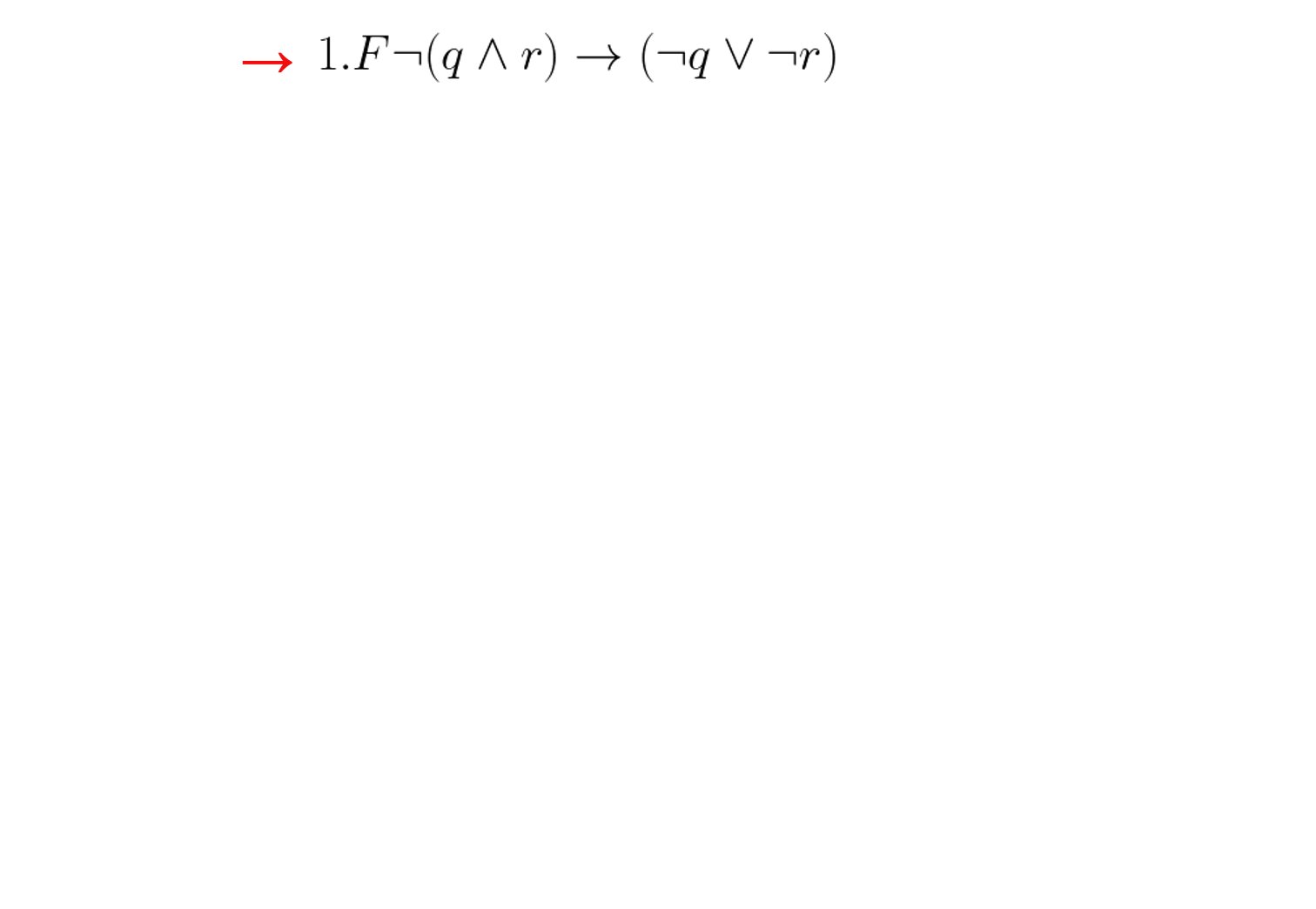
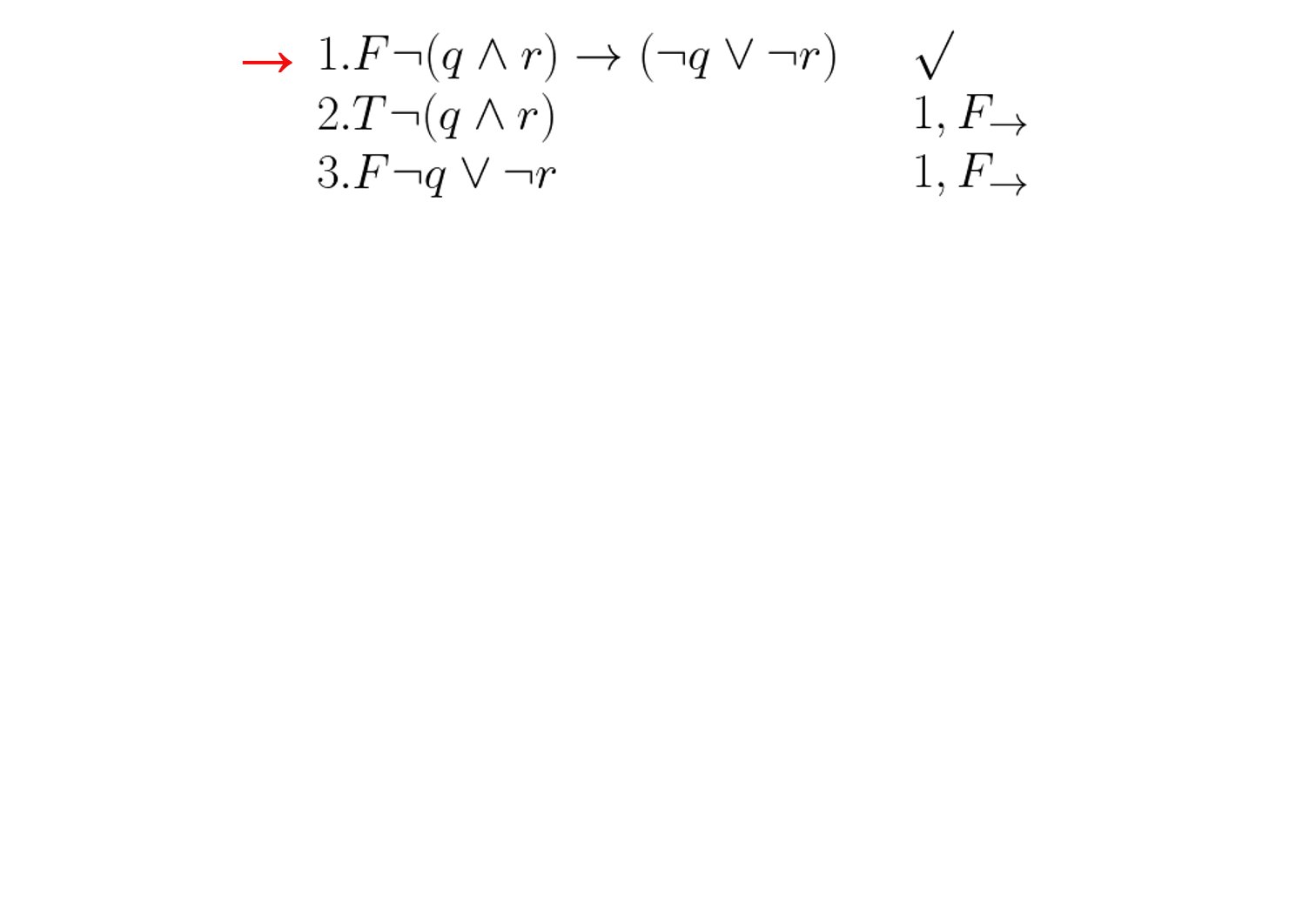
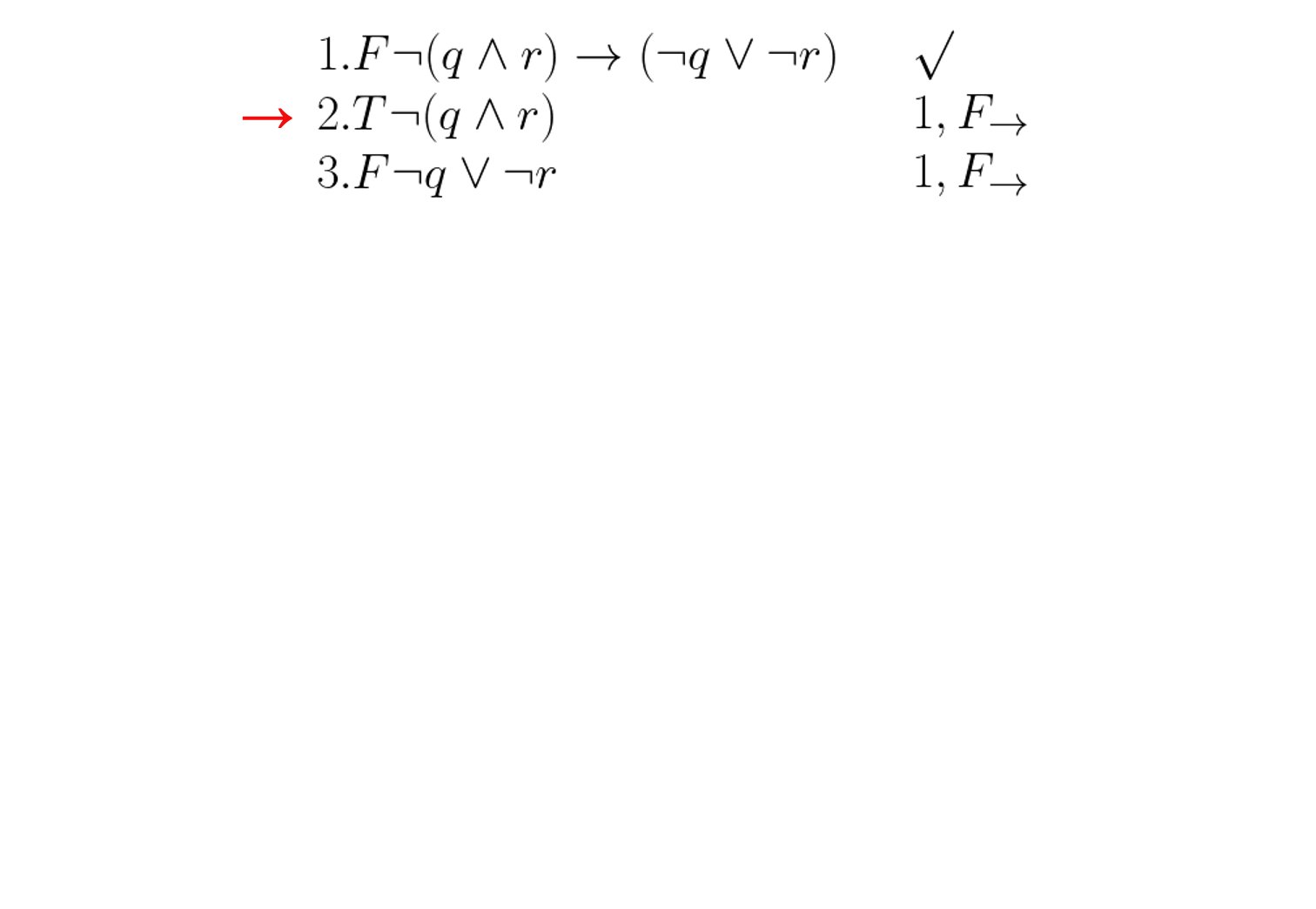
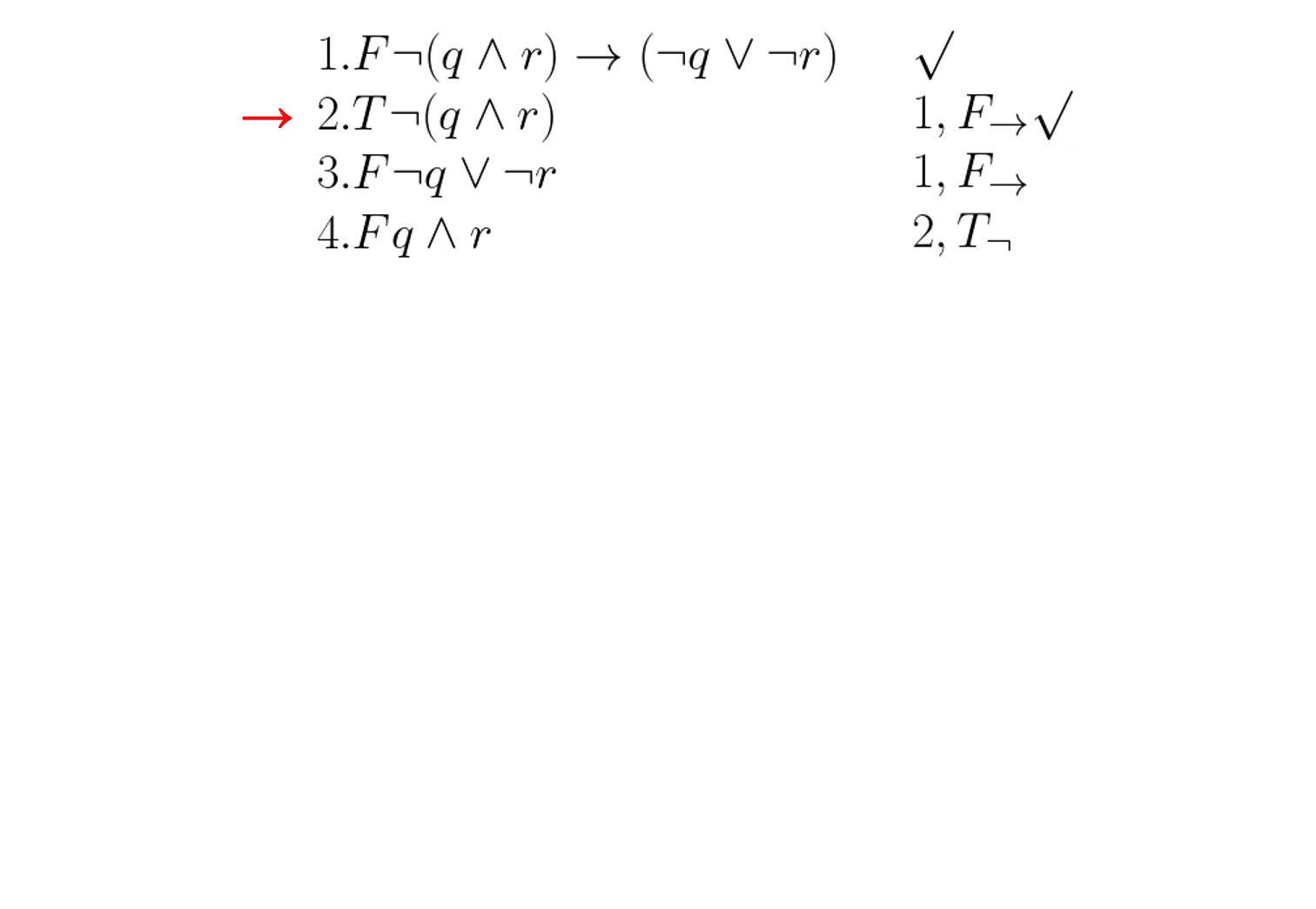
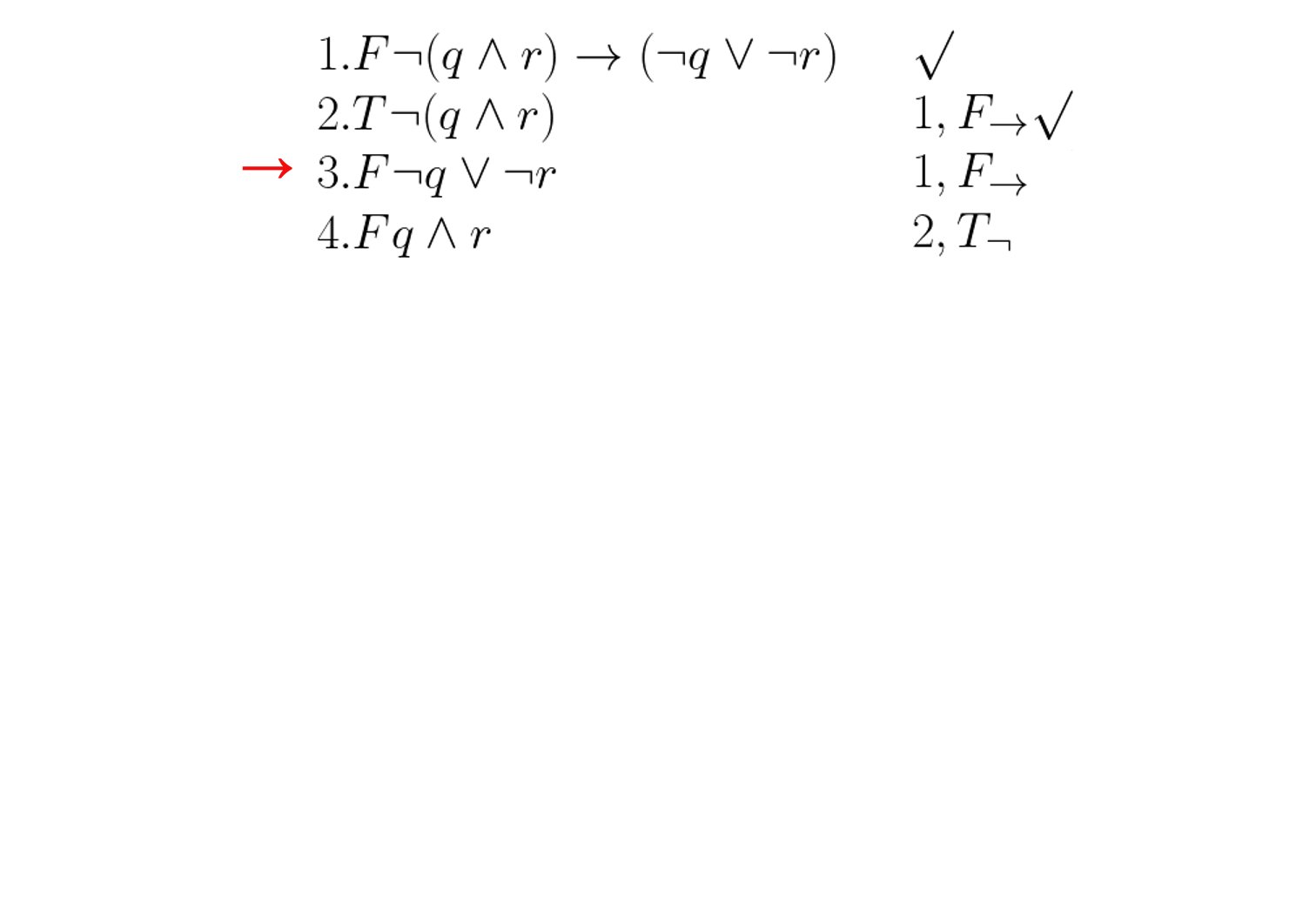
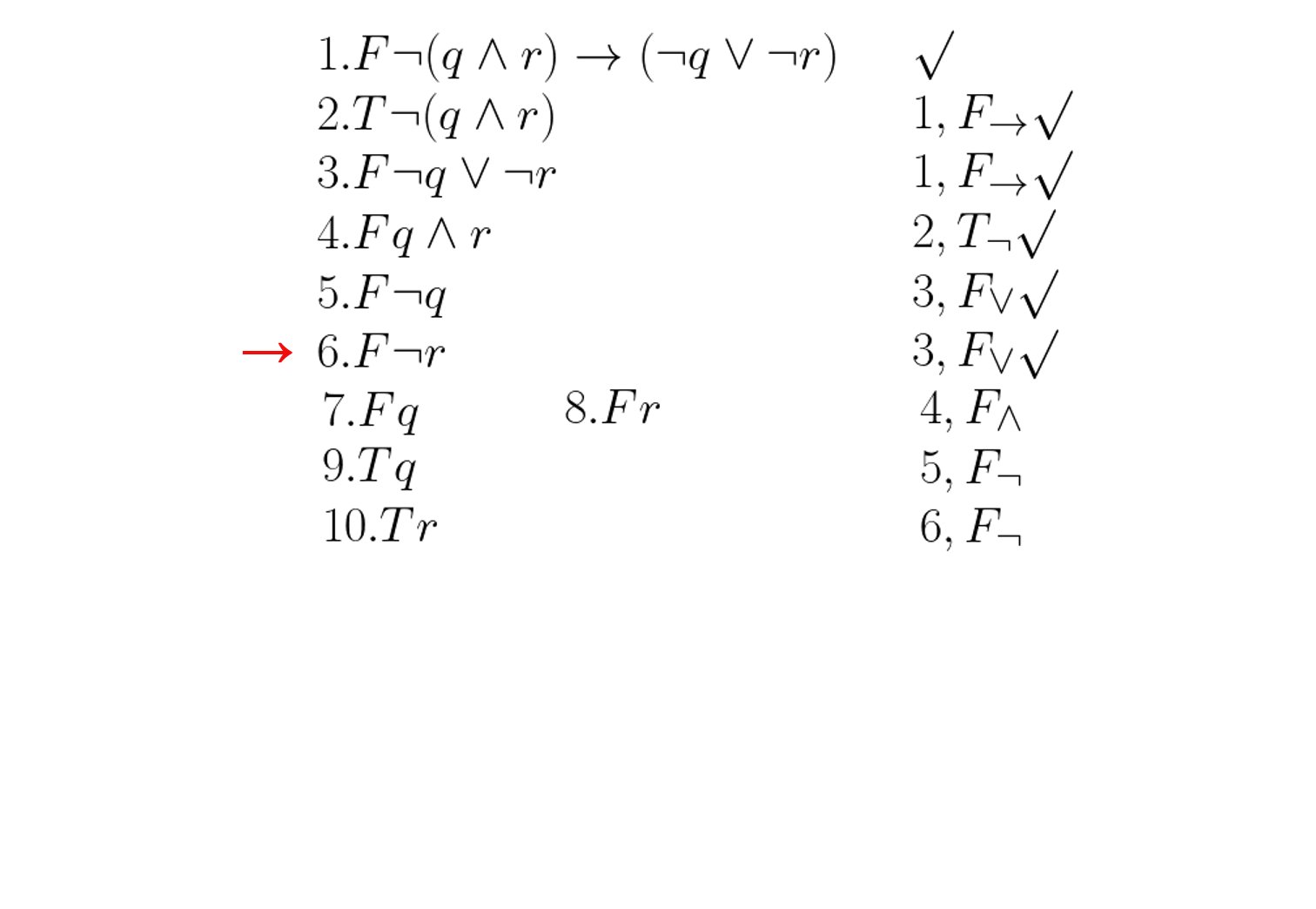
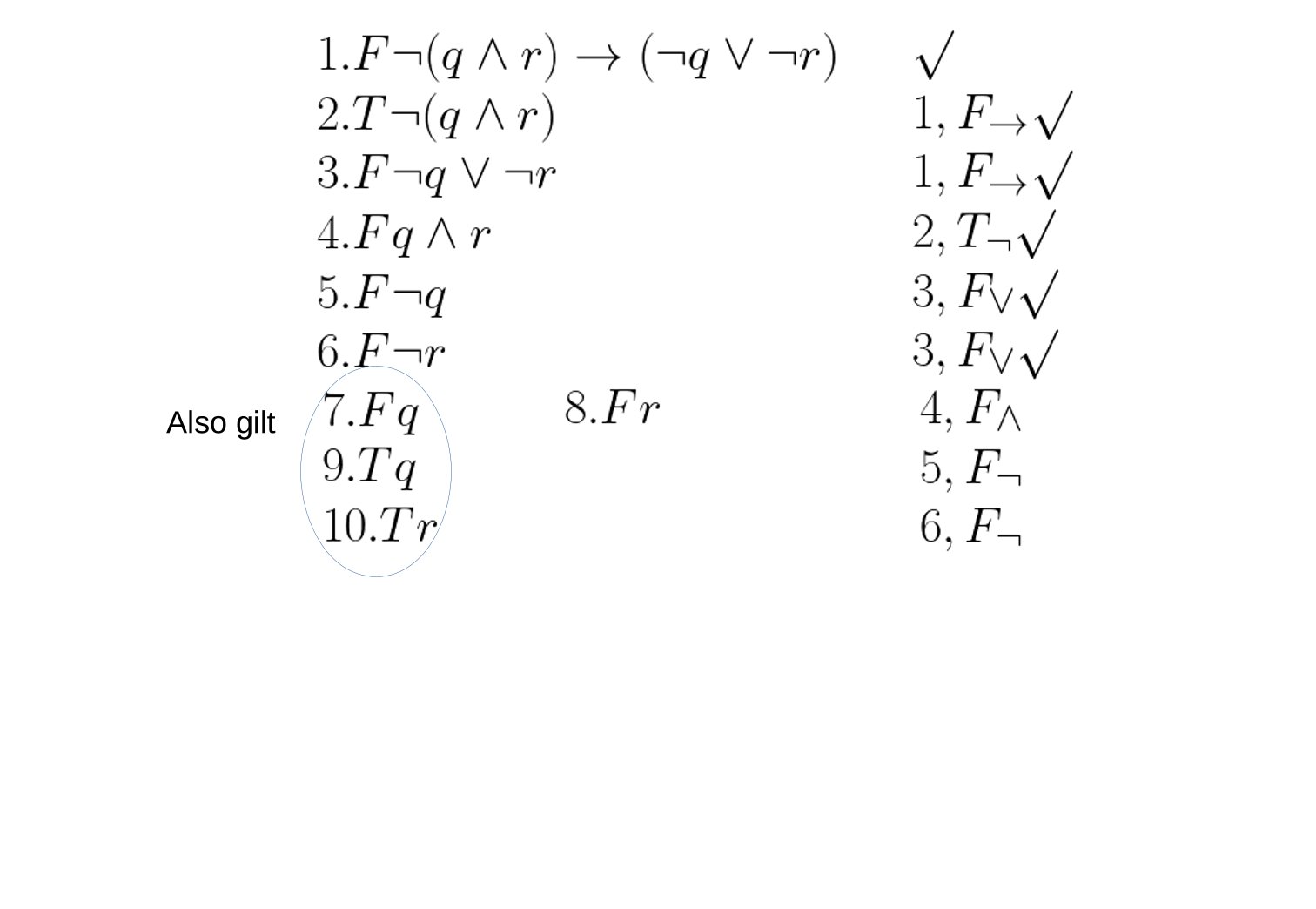
Beispiel 2:

Im folgenden soll die Gültigkeit von $(p \wedge q) \rightarrow (r\vee s)$ überprüft werden:

Procedure

• A (propositional) tableau is a tree, each of whose nodes is a signed (propositional) formula. A branch of a tableau is a branch of such a tree.
• We start with an initial tableau. This can be any tableau that has only a single branch.
• Tableau expansion works as follows. Given a tableau, try to find a node that (a) isn't a signed atomic formula, and (b) to which we haven't already applied an expansion rule (we call such nodes unexpanded nodes).
• If there are no unexpanded nodes, STOP! The tableau is rule saturated.
• If there are unexpanded nodes, chose one and apply the relevant expansion rule. That is, extend the tableau by adding on new nodes in the way demanded by the rule.

Tableau-provability

(© Patrick Blackburn & Johan Bos, slide 165)

Closed and open Tableau

• A branch of a tableau is closed if it contains both $T\phi$ and $F\phi$, where $\phi$ is some formula.
• A branch that is not closed is called open.
• A tableau is closed if every branch it contains is closed, and open if it contains at least one open branch.

(© Patrick Blackburn & Johan Bos, slide 166)

The key definition
A formula $\phi$ is tableau-provable (or, more simply: provable) if and only if it is possible to expand the initial tableau consisting of a single node$F\phi$ to a closed tableau. The notation $\vdash_{t}\phi$ means that $\phi$ is tableau-provable.

Übungen

Informativity Check

Implementing Tableau Method (BB: 4.3)

Übungen

Exercise 4.3.1 Try the prover out on some simple examples. Make sure you understand what is happening at each step. One way to do this is to use the standard Prolog trace/0, but a nicer way is to add the following code as a new second clause for the predicate closedTableau/1:

closedTableau(OldTableau):- nl,write(OldTableau),nl,fail.

Because this new clause always fails, it has no effect on the correctness of the predicate. However, before it fails it will write out the current state of the tableau, enabling you to follow the prover's progress easily.

Exercise 4.3.2 Try to find examples of theorems which the tableau prover can't handle, or can't handle fast. That is, try to find propositional formulas which you know to be valid but which the tableau prover either won't halt on, or takes a long time to halt. (The last two formulas in the test suite are like this, but try to find your own examples before looking at these.)

Exercise 4.3.3 Modify the code so that the tableau prover handles the bi-implication connective $\leftrightarrow$ (use, say, bimp/2 as the Prolog notation for this connective).

Zusatzaufgaben:

closedBranch: closedBranch/1 ist wie folgt definiert:

closedBranch(Branch):-
    memberList(t(X),Branch),
    memberList(f(X),Branch). 

Warum reicht es nicht, closedBranch/1 wie folgt zu definieren?

closedBranch(Branch):-
    memberList(t(X),Branch),
    memberList(t(not(X)),Branch).

Tableaus als verschachtelte Listen: Die Prolog-Notation für das Tableau mit den Formeln $f(p\rightarrow q),f(p\wedge q)$ sieht so aus: [[f(imp(p,q)), f(and(p,q), f(p)]]. Nach Anwendung der Regel $\rightarrow_{F}$ teilt sich das Tableau in zwei Subtableaus auf: [[f(and(p,q), f(p)],[f(and(p,q), t(q)]]. Der gemeinsame Teil vor der Verzweigung muss also wiederholt werden.

Alternativ könnte man das Tableau auch mit verschachtelten Listen darstellen [f(and(p,q), [[f(p)], [t(q)]]]. Dies ist jetzt eine Repräsentation ohne Redundanzen . Wenn man sich für diese Repräsentation entscheidet, welches Prädikat wird dann komplizierter? 

Zusatzaufgabe: Ändere die Implementierung so, dass sie mit verschachtelten Listen zur Repräsentation von Tableaubäumen arbeitet.

Tableau Provability: Schreiben sie ein Prädikat tmodels/2 welches die Relation $\phi_1,\dots,\phi_n\vdash_t\psi_1,\dots,\psi_n$ umsetzt. Die Argumente von tmodels/2 sollen Listen mit Formeln sein.

Resolution (BB: 4.4)

• Die Resolutionsmethode ist eine maschinenorientierte Methode. Anders als bei der Tableaux-Methode basiert die Resolution auf der wiederholten Anwendung nur einer einzigen Regel, der "Resolution Rule".
• Ein wichtiger Unterschied zur Tableaux-Methode ist, dass die Resolutionsregel nicht auf eine beliebige Input-Formel angewandt werden kann. Vielmehr muss die Input-Formel zunächst in eine äquivalente Formel in "Conjunctive Normal Form (CNF)" umgewandelt werden. Die Resolutionsregel operiert dann auf der CNF-Formel.
• Wie die Tableaux-Methode ist auch die Resolutionsmethode eine Beweismethode, die auf Widerlegung einer Formel basiert. Das heißt, um $\phi$ zu beweisen, geben wir $\neg \phi$ ein und zeigen, dass diese nicht erfüllbar ist.

Um die Gültigkeit einer Formel $\phi$ mit der Resolutionsmethode zu beweisen sind zwei Schritte erforderlich:

1. Wandle $\neg\phi$ in die Mengen-konjunktive-Normalform (setCNF) um.
2. Wende die Resolutionsregel wiederholt auf $\neg\phi$ in setCNF an, bis entweder eine leere Klausel entsteht ($\approx \phi$ ist gültig) oder keine Regelanwendung mehr möglich ist und keine Klausel leer ist ($\approx \phi$ ist nicht gültig).

Umwandlung einer Formel in setCNF

Definition: Conjunctive Normal Form (CNF)

• Ein (propositionales) Literal ist entweder ein Satzsymbol (z. B. $p,q,r,…$), oder die Negation eines Satzes (z. B. $\neg p, \neg q, \neg r,…$)
• Eine Klausel ist eine Disjunktion von Literalen (z.B. $(p \lor q \lor \neg r \lor s \lor \neg t)$) ist eine Klausel. Beachten Sie, dass wir, um eine Klausel wahr zu machen, einfach eines der darin enthaltenen Literale wahr machen müssen. Es gibt eine spezielle Klausel, die leere Klausel, manchmal auch $[ ]$ geschrieben, die niemals wahr gemacht werden kann.
• Eine Formel ist in CNF (Conjunctive Normal Form) wenn sie eine Konjunktion von Klauseln ist (z.B. $(p \lor q) \land (r \lor \neg p \lor s) \land (q \lor \neg s)$ ist in CNF. Beachte, dass eine CNF-Formel nur dann wahr sein kann, wenn alle darin enthaltenen Klauseln wahr sind.
• CNF Formeln haben eine sehr einfache Struktur und können als geschachtelte Listen geschrieben werden. Dabei wird z.B. $(p \lor q) \land (r \lor \neg p \lor s) \land (q \lor \neg s)$ als $[[p,q],[r,\neg p,s],[q,\neg s]]$ geschrieben.

Definition: setCNF

Eine CNF-Formel ist in set CNF, wenn in keiner Klausel ein Literal zweimal auftritt und keine Klausel (als Menge betrachtet) zweimal vorkommt. Wenn $C$ eine Klausel ist, schreiben wir set(C) für die Klausel in set CNF Form. Beispiel: $set([[p,q,p],[r,\neg p,s,r],[q,\neg s],[q,p]])=[[p,q],[r,\neg p,s],[q,\neg s]]$

Die Umwandlung einer Formel in setCNF erfolgt in 3 Schritten:
1. Umwandlung in Negative Normalform (NNF)
2. Umwandlung in Konjunktive Normaleform (CNF)
3. Umwandlung in mengenförmige konjunktive Normalform (setCNF)

Umwandlung in negative Normalform (NNF)

• Eine Formel ist in negativer Normalform, wenn nur aus Literalen, Klammern, Konjunktionen und Disjunktionen besteht (es erscheinen nur noch die Operatoren ∧ und ∨, Literale und Klammern).
• Um eine Formel in NNF zu transformieren, werden die folgenden Regeln wiederholt angewandt:
  1. Schreibe $\neg (\phi \land \psi)$ um zu $\neg \phi \lor \neg \psi$
  2. Schreibe $\neg (\phi \lor \psi)$ um zu $\neg \phi \land \neg \psi$
  3. Schreibe $\neg (\phi \rightarrow \psi)$ um zu $ \phi \land \neg \psi$
  4. Schreibe $(\phi \rightarrow \psi)$ um zu $\neg \phi \lor \psi$
  5. Schreibe $\neg \neg \phi$ um zu $\phi$

Frage: Wie heißen die ersten beiden Regeln?

Umwandlung NNF in CNF

• Um eine NNF-Formel in CNF zu transformieren, werden die folgenden Regeln wiederholt angewandt:
  1. Schreibe $ \theta \lor ( \phi \land \psi)$ um zu $(\theta \lor \phi) \land (\theta \lor \psi)$
  2. Schreibe $(\phi \land \psi) \lor \theta$ um zu $(\phi \lor \theta) \land (\psi \lor \theta)$
  3. Schreibe $(\phi \land \psi) \land \theta$ um zu $ \theta \land ( \phi \land \psi)$
  4. Schreibe $(\phi \lor \psi) \lor \theta$ um zu $ \theta \lor ( \phi \lor \psi)$
• Beachte die Wirkung der ersten beiden Umschreibregeln: Sie treiben Vorkommen von $\lor$ tiefer in die Formel und "heben" Vorkommen von $\land$. Das ist das, was wir für CNF wollen.

Frage: Wie heißen die Gesetze für die ersten beiden und die zweiten beiden Regeln?

Umwandlung CNF in setCNF

Eine CNF-Formel ist in set CNF, wenn in keiner Klausel ein Literal zweimal auftritt und keine Klausel zweimal vorkommt. Wenn $C$ eine Klausel ist, schreiben wir set(C) für die Klausel in set CNF Form.

Aufgabe: Wandle die folgende Formel in set CNF um:

$$p \rightarrow (p \wedge (q \vee \neg p))$$

Resolutionsregel

Aus:

$$[p_1 ,..., p_n, R, p_{n+1} , ..., p_m ]$$ und $$[q_1, ..., q_j , \neg R, q_{j+1}, ..., q_k ]$$

können wir

$$ [p_1 ,..., p_n, p_{n+1}, ..., p_m, q_1 , ..., q_j , q_{j+1} , ..., p_k]$$ deduzieren.

• Die Resolutionsregel basiert darauf, dass aus den beiden Klauseln $[p_1 ,…, p_n, R, p_{n+1} , …, p_m ]$ und $[q_1, …, q_j , \neg R, q_{j+1}, …, q_k ]$ die Klausel $ [p_1 ,…, p_n, p_{n+1}, …, p_m, q_1 , …, q_j , q_{j+1} , …, p_k]$ logisch folgt.
• Beispiel: aus $[p,s,\neg t,r]$ und $[q,v,\neg s, r]$ können wir $[p, \neg t, r, q, v, r]$ deduzieren.

FRAGE: Ist die Anwendung der Resolutionsregel eine Äquivalenzumformung?

Terminologie: $R$ und $\neg R$ heißen complementary pair und die beiden Klauseln complementary clauses.

Resolution verwenden

• Wir negieren die Formel, die wir zu beweisen versuchen, und wandeln sie in setCNF um.
• Dann wenden wir die Resolutionsregel so lange auf die Klauseln der setCNF-Formel an, bis wir sich entweder nichts mehr ändert (also keine neuen Klauseln mehr entstehen), oder bis die leere Klausel erzeugt wurde.
• Bei der Anwendung der Resolutionsregel fügen wir die durch die Resolution gewonnenen neuen Klauseln zu den alten hinzu.
• Nach dem Hinzufügen einer Klausel bringen wir unsere Formel wieder in setCNF-Form. Sprich wir entfernen doppelte Elemente in einer Klausel und doppelte Klauseln.
• Wenn wir während dieses Prozesses eine leere Klausel erzeugen, zeigt dies, dass $\neg \phi$ nicht konsistent ist (warum?), und somit dass $\phi$ gültig ist.

Ein simples Beispiel: Der Beweis von $p \lor \neg p$

• Zuerst negieren wir $p \lor \neg p$ und erhalten $\neg(p \lor \neg p)$
• Dann bringen wir $\neg (p\lor \neg p)$ in CNF und erhalten $ [[\neg p],[p]]$.
• eine Anwendung der Resolutionsregel bringt direkt $[[]]$.
• Daher ist $\neg(p \lor \neg p)$ nicht konsistent.
• Daher ist $p \lor \neg p$ valide.

Aufgaben:

1. Zeige mit der Resolutionsmethode, ob $p \rightarrow (p \vee q)$ gilt.
2. Zeige mit der Resolutionsmethode, ob $p \rightarrow (q \rightarrow p)$ gilt.
3. Zeige mit der Resolutionsmethode, ob $(p\vee q) \rightarrow p$ gilt.

Implementing Resolution

Theoretical Remarks

Soundness: Ein Beweissystem ist sound, wenn jede Aussage, die beweisbar ist, auch gültig ist. Wenn $\vdash \phi$ dann $\vDash \phi$

Completeness: Ein Beweissystem ist complete, wenn jede Aussage, die gültig ist, auch beweisbar ist. Wenn $\vDash \phi$ dann $\vdash \phi$

Theorem (Resolutionsmethode): Die Resolutionsmethode für die Aussagenlogik ist sound und complete.

Theorem (Tableaumethode): Die Tableaumethode für die Aussagenlogik ist sound und complete.

Entscheidbarkeit: Eine Menge heißt entscheidbar, wenn es einen Algorithmus gibt, der für jedes Objekt entscheidet, ob das Objekt zur Menge gehört oder nicht.

Aussagelogik: Die Menge der gültigen aussagenlogischen Formeln ist entscheidbar.

Erklärvideo

Film zum Resolutions- und Tableauverfahren in der Aussagenlogik