Computational Semantics
Tutorial

Chapter 3: Underspecified Representations

Scope Ambiguities (BB: 3.1)

Beispiele:

  • Jeder Mann liebt einen Hund. (2 Lesarten)
  • Jeder Hund jagt eine Katze in jedem Zimmer.

Aufgaben:

  • Gib für die Beispiele jeweils alle Lesarten an.
  • Wähle für jede Lesart des zweiten Satzes ein Modell mit 2 Katzen, 2 Hunden und 2 Zimmern, so dass die Aussage in dem Modell erfüllt ist.

Terminology:

  • has scope over / out-scopes
  • narrow scope vs. wide scope
  • weak vs. strong reading
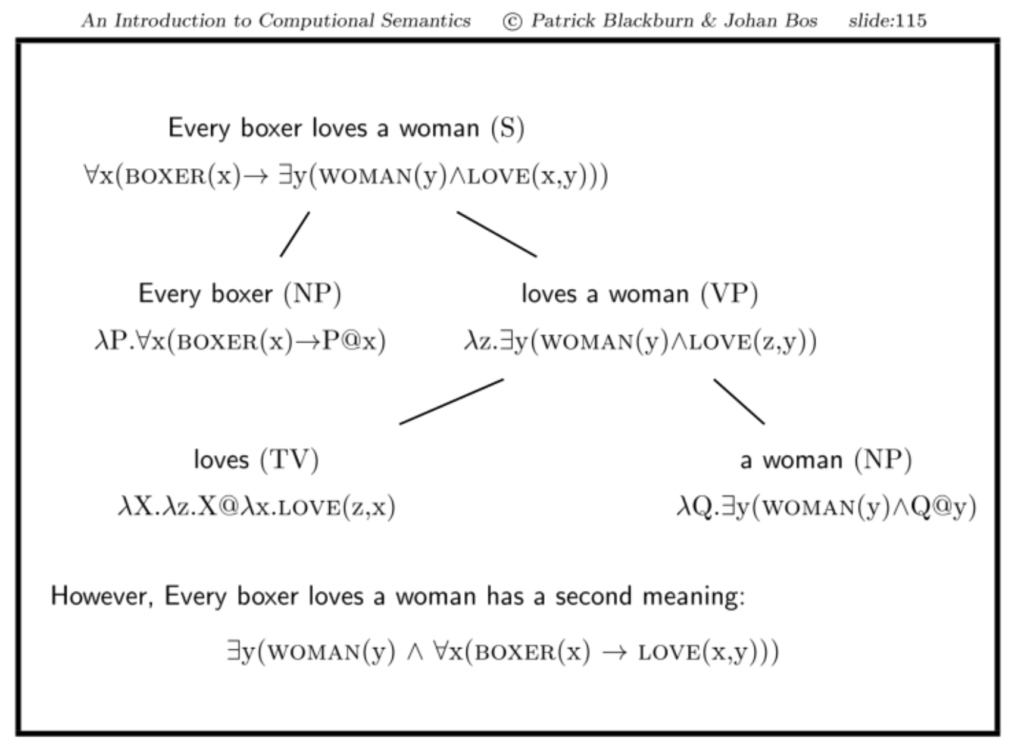
  • Warum bekommen wir mit unserem bisherigen Vorgehen immer nur eine Lesart?
  • Bekommen wir die schwächere oder die stärkere Lesart?

Every owner of a hash bar gives every criminal a big kahuna burger.

18 Lesarten:

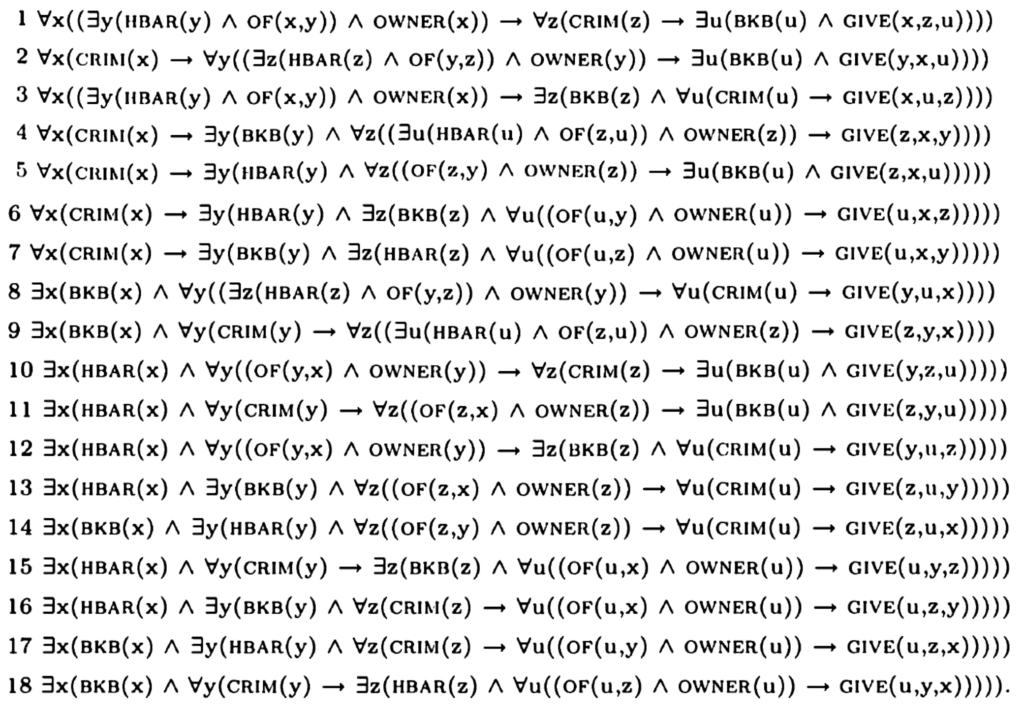
Einige Lesarten sind äquivalent, andere implizieren einander. Die Lesarten zerfallen in zwei logisch unabhängige Gruppen:

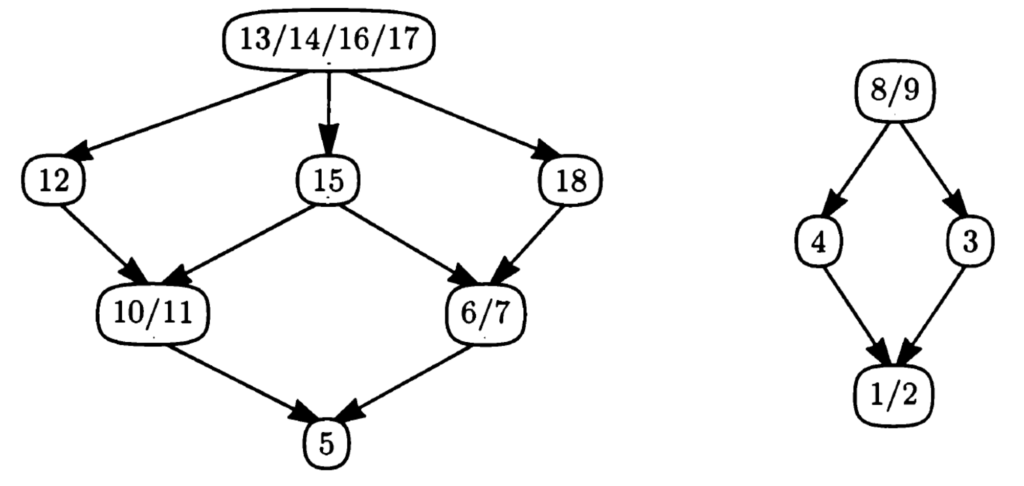
Montague’s Approach (BB: 3.2)

Quantifier Raising (Montagues Trick):

  • Quantifizierte NPs werden zunächst durch indizierte Pronomen ersetzt
  • Die indizierten Pronomen dienen als Platzhalter und werden ganz normal verarbeitet
  • Wenn der Platzhalter (das indizierte Pronomen) weit genug im Syntaxbaum nach oben durchgereicht wurde, wird er wieder durch die quantifizierte NP ersetzt.

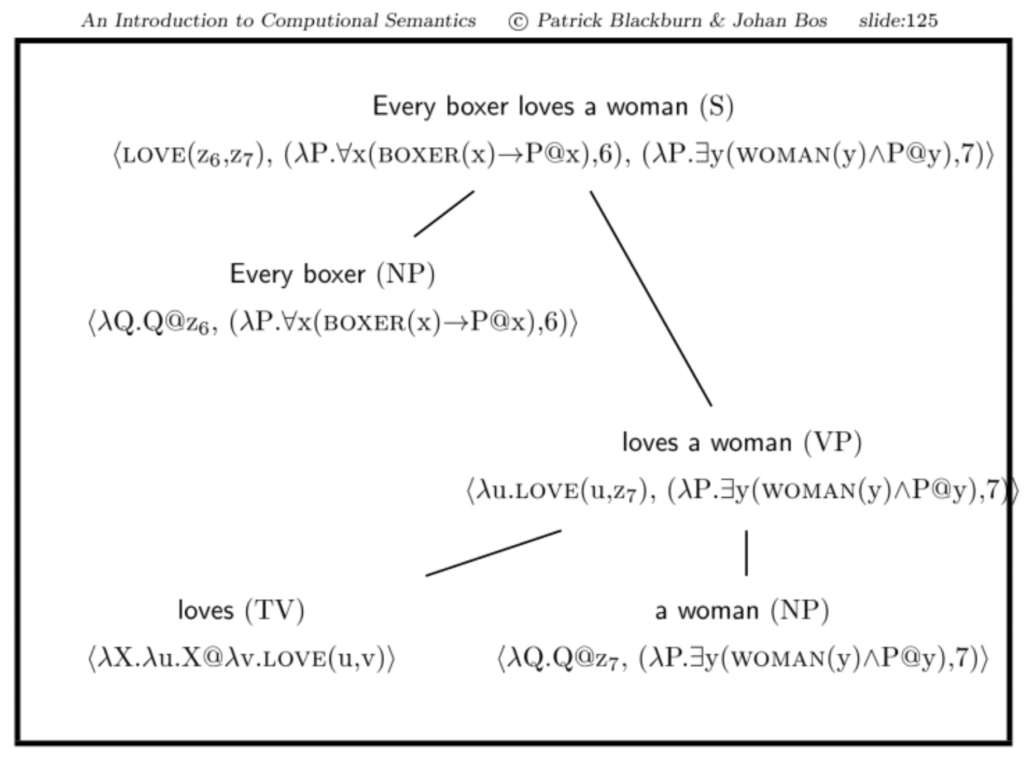
Beispiel: Every boxer loves a woman

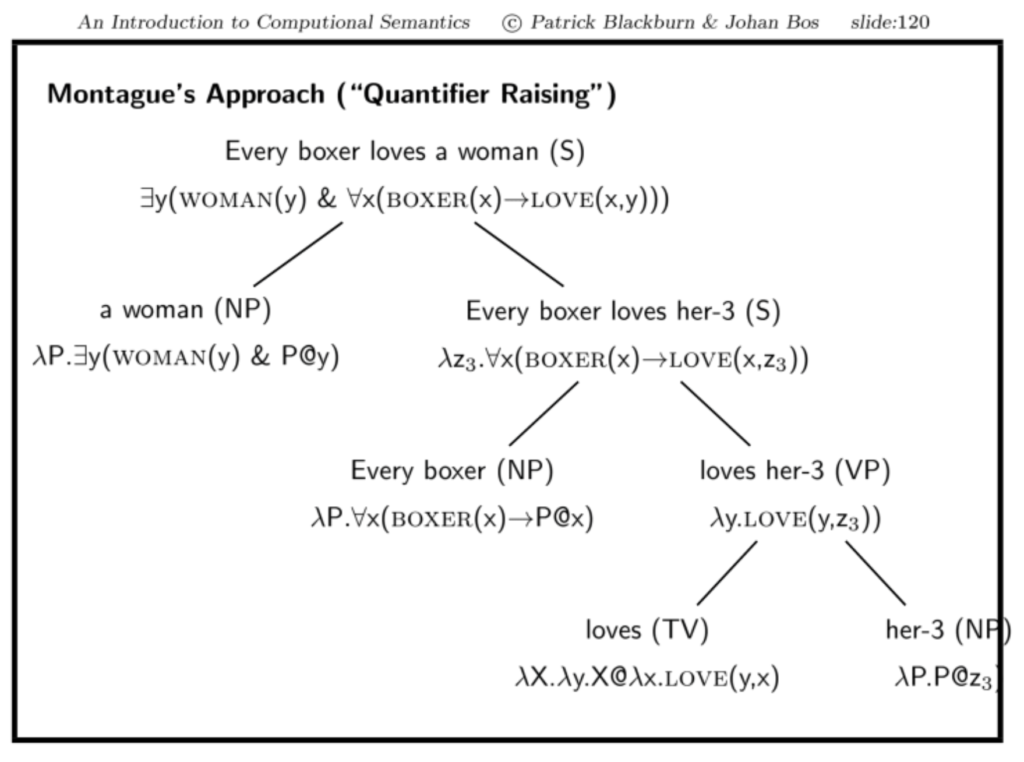
  • an die Stelle der quantifizierten NP a woman tritt zunächst das indizierte Pronomen her-3 mit einer entsprechend indizierten Variable z3 als Platzhalter.
  • Dieses wird im Syntaxbaum nach oben durchgereicht.
  • Abschließend wird es durch die quantifizierten NP ersetzt, indem die indizierte Variable Lambda-abstrahiert wird.
  • Hierbei dient die quantifizierten NP als Funktor und die Lambda-Abstraktion des Ausdrucks mit der indizierten Variable als Argument.

Bewertung des Ansatzes:

  • Die Grundidee ist gut. Insbesondere die Idee, dass wir eine Dummy-Semantikrepräsentation haben, die wir bei Bedarf abrufen, ist gut.
  • Aber die Art und Weise, wie Montague diese Idee umsetzt, ist ungünstig. Sie belastet die Grammatikregeln stark. Wir wollen nicht mit der Grammatik spielen – wir wollen die semantische Konstruktion an bestehende Grammatiken ‚anschrauben‘.
  • Die Storage Methods verschieben im Wesentlichen die Kernidee von Montagues Ansatz aus der Syntax in die semantische Konstruktionskomponente.

Storage Methods (BB: 3.3)

Cooper Storage

Grundlagen

Kernideen:

  • jedem Knoten des Syntaxbaums wird ein Speicher zugeordnet.
  • der Speicher enthält eine „Kern“-Semantikrepräsentation zusammen mit den Quantoren, die mit Knoten tiefer im Baum verknüpft sind.
  • nachdem der Satz geparst wurde, wird der Speicher verwendet, um Repräsentationen mit Quantoren zu erlangen.
  • die Reihenfolge, in der der Speicher abgerufen wird, bestimmt den Skopus der Quantoren

Speicher formaler:

  • ein Speicher ist eine Liste und wird durch spitze Klammern dargestellt:〈 und 〉
  • das erste Element der Liste ist die semantische Kernrepräsentation der durch den Knoten repräsentierten Konstituente
  • nachfolgende Elemente sind Paare $(\beta,i)$, wobei $\beta$ die semantische Repräsentation einer NP und $i$ ein Index ist
  • ein Index ist ein Label, das eine freie Variable in der semantischen Kernrepräsentation herausgreift
  • Die Paare $(\beta,i)$ heißen indizierte Bindungsoperatoren (indexed binding operators)

Speicheraufbau (Cooper)

Cooper Storage Definition (Speicher-Regel):

Wenn der Speicher〈φ, $(\beta,j),…, (\beta$‘,$k)$ 〉eine semantische Repräsentation für eine quantifizierte NP ist und wenn $i$ ein eindeutiger Index im Syntaxbaum ist, dann ist der Speicher〈λP.P@zᵢ, (φ,$i$), $(\beta,j),…, (\beta$‘,$k)$ auch eine Repräsentation für diese NP.

Was folgt aus der Definition?

  • Nur quantifizierte NP’s können den Speicher verändern.
  • Die Speicher-Regel ist eine kann-Regel: Trifft man auf eine quantifizierte NP hat man die Wahl
    1. der Store bleibt unverändert und die Semantik der NP wird direkt in die Repräsentation eingebaut
    2. es wird ein Platzhalter gesetzt und die Semantik der NP für die spätere Verarbeitung im Speicher gespeichert.
  • Der Ausdruck $\lambda P.P @ z_i$ entspricht der Semantik der indizierten Pronomen von Montague. Eine quantifizierte NP wie a woman kann also auf zwei Arten repräsentiert werden
    1. $\langle \lambda P. \exists y (\text{woman}(y) \wedge P @ y) \rangle$
    2. $\langle \lambda Q. Q @ z_7, (\lambda P. \exists y (\text{woman}(y) \wedge P @ y),7) \rangle$
  • Trifft innerhalb des Ableitungsbaums ein Funktor $\langle \phi, (\alpha,j),\ldots (\alpha$‘,$k)\rangle$ auf ein Argument $\langle \psi, (\beta,l),\ldots (\beta$‘,$m)\rangle$, so ist der Speicher des Mutterknotens $\langle \phi @ \psi, (\alpha,j),\ldots (\alpha$‘,$k),(\beta,l),\ldots (\beta$‘,$m)\rangle$.

Speicherabbau / Retrieval (Cooper)

Retrieval

Um den Speicher wieder aufzulösen, müssen die gespeicherten quantifizierten NP’s in die Kernrepräsentationen eingesetzt werden. Dies geschieht, indem wir

  • einen der indizierten Bindungsoperatoren aus dem Speicher entfernen
  • und mit der Kernrepräsentation kombinieren.
  • das Ergebnis ist eine neue Kernrepräsentation.
  • Dieser Vorgang wird fortgesetzt, bis der Speicher nur noch die Kernrepräsentation enthält, sprich bis alle Bindungsoperatoren abgearbeitet sind.

genauer gesagt:

Coopers Retrieval-Regel:

Seien σ₁ und σ₂ (möglicherweise leere) Sequenzen von Bindungsoperatoren. Wenn der Speicher 〈φ, σ₁, $(\beta,i)$, σ₂〉 einem Ausdruck der Kategorie S zugeordnet ist, dann ist der Speicher 〈$\beta @ \lambda $zi.φ, σ₁, σ₂〉auch diesem Ausdruck zugeordnet.

Implementing Cooper Storage

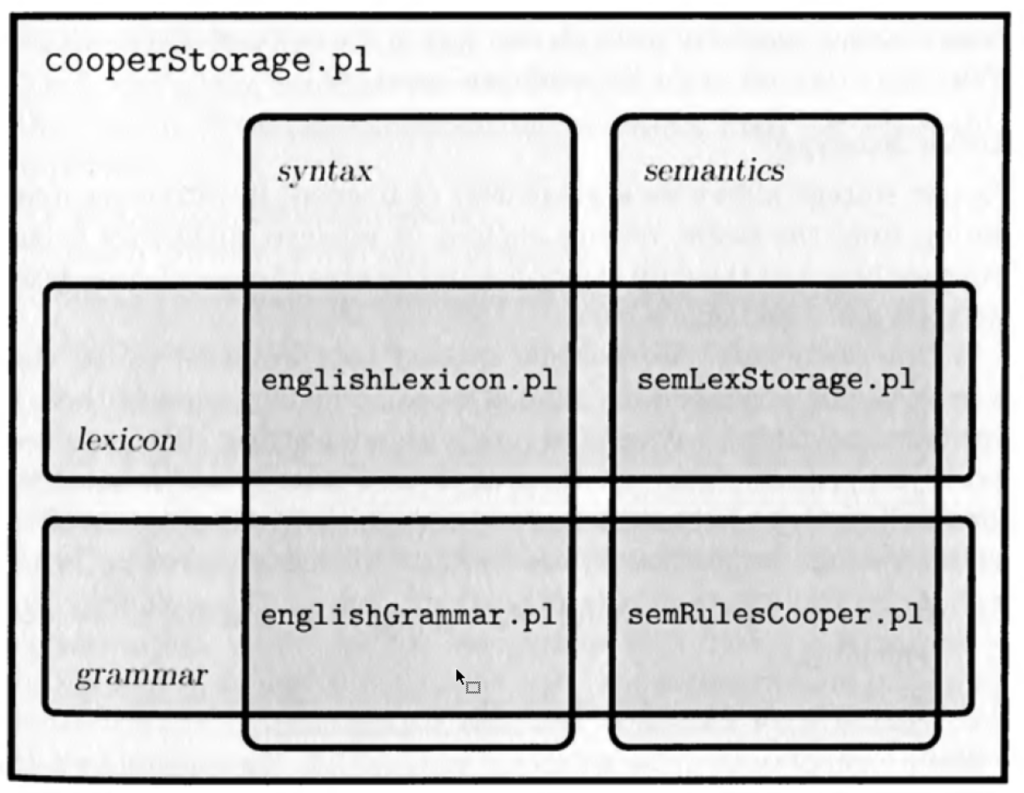
Aufgaben:

  • Lade cooperStorage.pl und teste ein paar Sätze. Denkt dran, mit =infix.= könnt ihr die Ergebnisse in der Infixnotation sehen.
  • Wie viele Ergebnisse erhältst du für ‚every boxer loves a person‘?
  • Kommentiere in cooperStorage/0 die Verwendung von filterAlphabeticVariants/2 aus und schreibe stattdessen Sems1=Sems2. Wie viele Ergebnisse erhältst du für ‚every boxer loves a person.‘? Warum?
  • Teste auch Negation ‚every boxer does not love a criminal‘. Sind die Ergebnisse vollständig und korrekt?
  • In der Implementierung besteht optional die Möglichkeit die Semantik der NP direkt an der Stelle ihres Vorkommens im Ableitungsbaum zu verarbeiten. Ändere die Dateien so, dass die NP immer zunächst in den Speicher geschrieben wird und erst am Ende verarbeitet wird. Teste einige Sätze mit mehreren quantifizierten Phrasen und Negation. Was fällt dir auf? Sammle Beispiele, die zeigen, warum es wichtig ist, dass die Speicherregel optional ist.
  • Diskutiere die Ergebnisse aus der SentenceTestSuite und ergänze sie um problematische Sätze.
  • Sammle Sätze, die zu unvollständigen oder falschen Ergebnissen führen. Schreibe sie ins Etherpad.

Keller Storage

Wir haben gesehen, dass wir manchmal zu viele Analysen mit dem Cooper Storage erhalten.

?- cooperStorage.
  
> mia knows every owner of a hash bar.
  
1 all A ((some B (hashbar(B) & of(A,B)) & owner(A)) > know(mia,A))
2 all A ((of(A,B) & owner(A)) > some C (hashbar(C) & know(mia,A)))
3 some A (hashbar(A) & all B ((of(B,A) & owner(B)) > know(mia,B)))
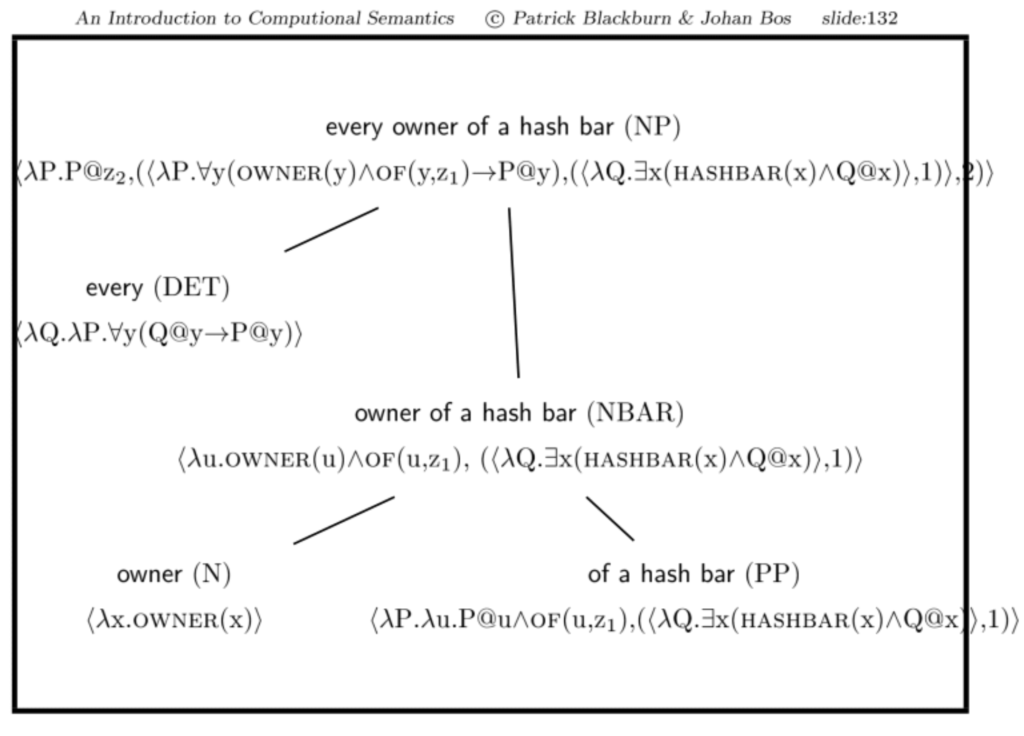
true.

Das Problem ist, dass wir es mit verschachtelten NP’s zu tun haben: ‘a hash bar’ ist eine sub-NP von ‘every owner of a hash bar’.

Cooper Storage ignoriert verschachtelte NP’s.

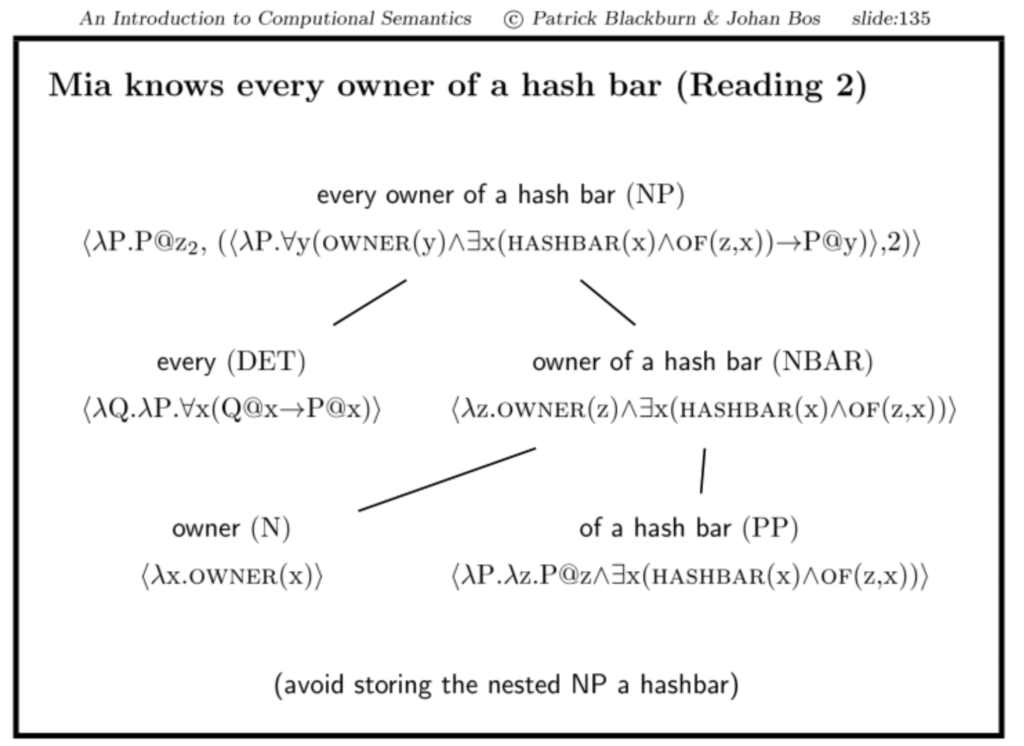
Implementing Keller Storage

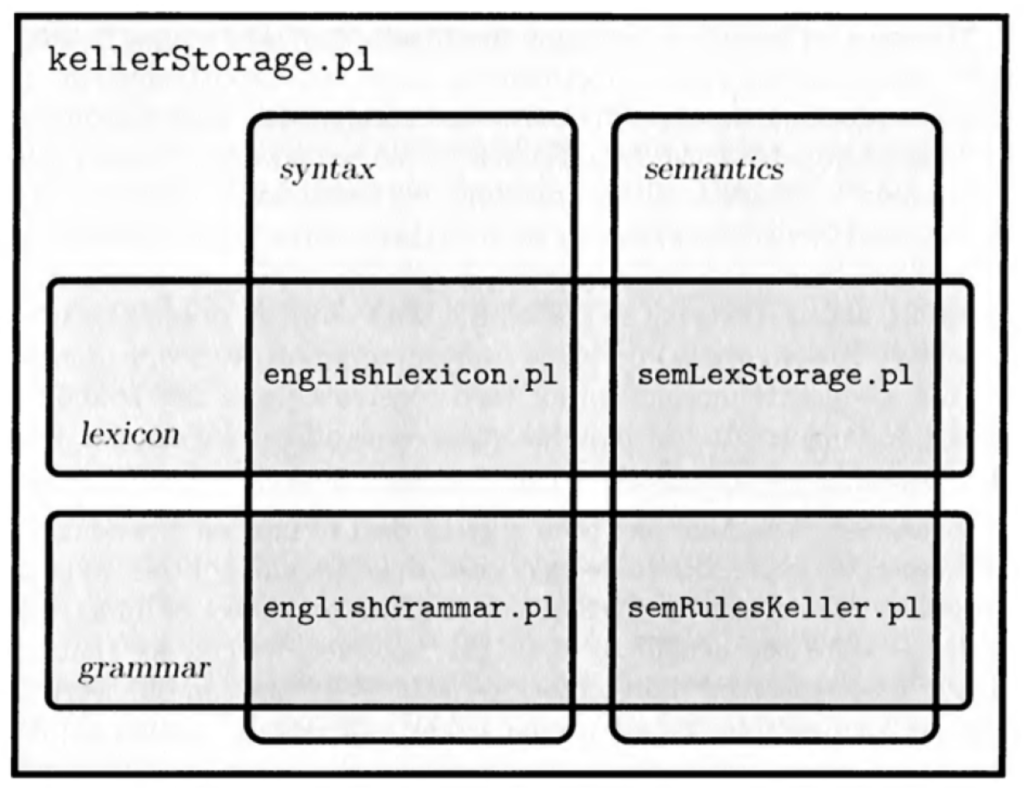
Die Dateien englishGrammar.pl und englishLexicon.pl bleiben wie gehabt unverändert. Auch an den semantischen Makros muss nichts verändert werden (semLexStorage.pl).

Nur die semantischen Regeln müssen angepasst werden, sie stehen jetzt in semRulesKeller.pl:

combine(np:[lam(P,app(P,X)),bo([app(A,B)|S],X)],[det:[A],n:[B|S]]).
combine(np:[app(A,B)|S],[det:[A],n:[B|S]]).

 % compare semRulesCooper.pl:
 % combine(np:[lam(P,app(P,X)),bo(app(A,B),X)|S],[det:[A],n:[B|S]]).
 % combine(np:[app(A,B)|S],[det:[A],n:[B|S]]).

Die Hauptatei ist kellerStorage.pl. Es gibt gegenüber cooperStorage.pl nur eine kleine Anpassung von sRetrieval/2

sRetrieval([S],S).
sRetrieval([Sem|Store],S):-
    selectFromList(bo([Q|NestedStore],X),Store,TempStore),
    appendLists(NestedStore,TempStore,NewStore),
    sRetrieval([app(Q,lam(X,Sem))|NewStore],S).

% compare cooperStorage.pl
% sRetrieval([S],S).
% sRetrieval([Sem|Store],S):-
%    selectFromList(bo(Q,X),Store,NewStore),
%    sRetrieval([app(Q,lam(X,Sem))|NewStore],S).

Aufgabe:

  • Lade kellerStorage.pl und teste ein paar Sätze. Denkt dran, mit =infix.= könnt ihr die Ergebnisse in der Infixnotation sehen.
  • Wie viele Ergebnisse erhältst du für ‘every boxer loves a criminal’?
  • Teste auch Negation ‘every boxer does not love a criminal’. Sind die Ergebnisse vollständig und korrekt?
  • Welche Lesarten erhältst du für ‘mia knows every owner of a hash bar.’?
  • In der Implementierung besteht optional die Möglichkeit die Semantik der NP direkt an der Stelle ihres Vorkommens im Ableitungsbaum zu verarbeiten. Ändere die Dateien so, dass die NP immer zunächst in den Speicher geschrieben wird und erst am Ende verarbeitet wird. Teste einige Sätze mit mehreren quantifizierten Phrasen und Negation. Was fällt dir auf? Sammle Beispiele, die zeigen, warum es wichtig ist, dass die Speicherregel optional ist.
  • Sammle Sätze, die zu unvollständigen oder falschen Ergebnissen führen. Schreibe sie ins Etherpad.
  • Zusatzaufgabe: Erweitere die Grammatik um ditransitive Verben (give/gives). Teste den Satz ‘every boxer gives every criminal a foot massage’. Sind die Analysen korrekt?

Probleme mit Storage Methods

  • Nicht ausdrucksstark genug (es gibt keine direkte Möglichkeit, bestimmte Lesarten auszufiltern).
    Beispiel: Der Satz „mia or a man dances“ erhält zwei Lesarten, nur die erste ist erwünscht:
    1. (dance(mia) v some A (man(A) & dance(A)))
    2. some A (man(A) & (dance(mia) v dance(A)))
  • Negation kann auch zu Skopus-Ambiguität führen, wird aber nicht korrekt behandelt.
    Beispiel: Der Satz „every boxer does not die“ erhält nur die Lesart
    „all A (boxer(A) > ~ die(A))“.
    Die Lesart „~ all A (boxer(A) > die(A))“ fehlt.
  • Für die Negation würde man einen zusätzlichen Skopus-Mechanismus brauchen (das ist nicht erwünscht)
  • Keine einfache Möglichkeit, Constraints (Einschränkungen) auf den Lesarten zu haben

Hole Semantics (BB: 3.4)

Ideen:

  • Wie bei den Storage-Methoden wird einem Satz an der Spitze des Ableitungsbaums eine unterspezifizierte semantische Repräsentation (USR) zugeordnet.
  • eine USR in Hole Semantik ist eine Menge von Constraints (constraint-basierter Ansatz)
  • jede logische Formel, die die Constraints in der USR erfüllt ist eine zulässige semantische Repräsentation des Satzes.
  • die Storage-Methoden sind nicht constraint-basiert sondern generierend: aus dem Storage (USR) lassen sich die semantischen Repräsentationen berechnen.

Prädikatenlogische Ausdrücke werden auf zwei Ebenen verwendet:

  • für die SRL (semantic representation language): Die Sprache in der wir die semantischen Repräsentationen der sprachlichen Ausdrücke formulieren (Prädikatenlogik 1. Stufe erweitert um den Lambdaoperator)
  • für die URL (underspecified representation langauge): Die Sprache in der wir die Constraints über Ausdrücke in SRL formulieren (Prädikatenlogik 1. Stufe mit Sorten)

Die semantischen Repräsentationen (sprich die prädiktenlogischen Formeln) werden dabei als Bäume aufgefasst und in der URL werden Constraints über diese Bäume ausgedrückt.

Beispiel zur Motivation:

Der Satz “every boxer loves a woman” hat zwei Lesarten, zu denen die folgenden Formeln und Bäume gehören:

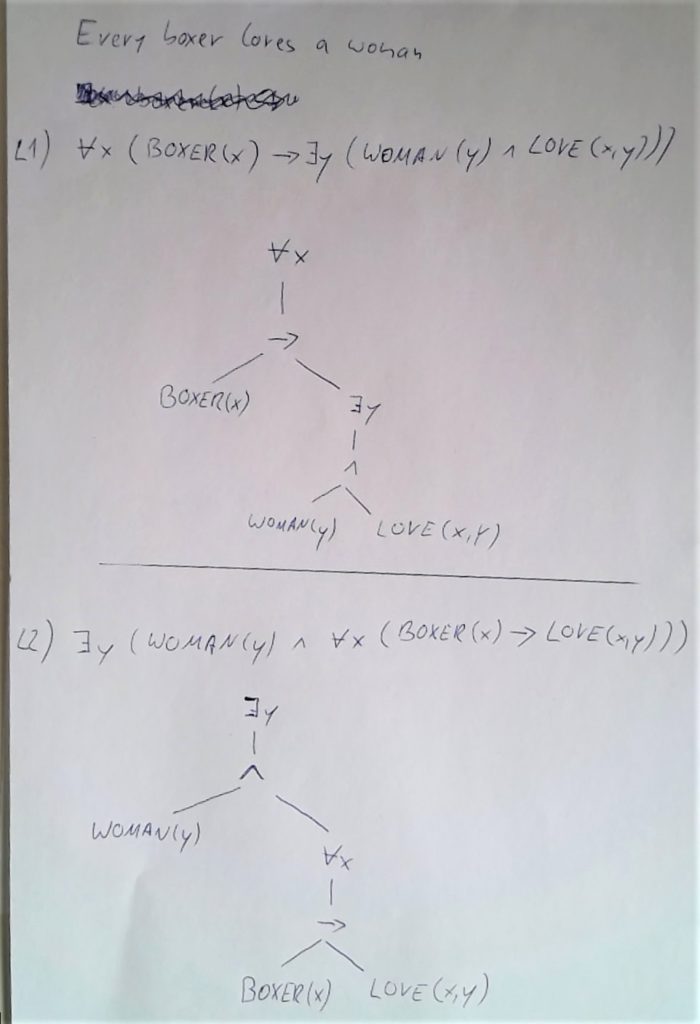
Diese beiden Bäume werden repräsentiert durch folgende unterspezifizierte Repräsentation:

Um aus einer solchen underspecified representation eine specified semantic representation zu erlangen, müssen den Löchern $h_i$ Labels zugewiesen werden $l_j$. Diesen Vorgang nennt man Plugging. Ein Plugging ist eine injektive Funktion von der Menge der Löcher in die Menge der Labels. Hier ein exemplarisches Plugging, für das Beispiel von oben:

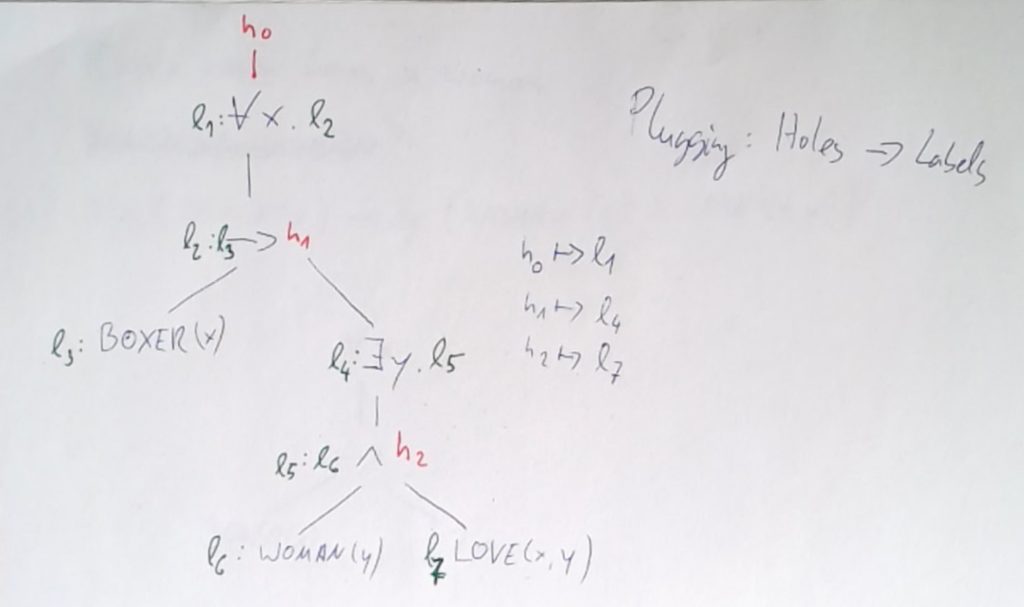
Underspecified Representation Languages (URLs)

Zunächst werden die Underspecified Representation Lanuages definiert, sprich die sprachen in denen die unterspezifizierten Repräsentationen geschrieben werden. Es gibt zu jeder semantischen Repräsentationssprache (SRL) eine URL, da das Vokabular der SRL in der URL reflektiert werden muss, um über die SRL sprechen zu können. Zu URLs:

  • URLs sind Sprachen erster Ordnung mit Sorten
  • „URLs are designed for talking about the way the subformulas that make up an SRL formula are embedded inside one another“
  • Mit URLs kann man die formula trees (Formelbäume) beschreiben

Vokabulare von URLs:

Alle logischen Operatoren sowie die (Prädikats)konstanten der SRL werden in der korrespondierenden URL abgebildet. Die Stelligkeit in der URL ist dabei jeweils um 1 höher als in der SRL, da ein Extraargument für den Label des Ausdrucks eingeführt wird.

  • Die Variablen einer URL werden Sorten zugeordnet. Dabei stehen $h,h$‘,$h_i,\ldots$ für Löcher (holes), $l,l$‘,$l_i,\ldots$ für Labels und $v,v$‘,$v_i,\ldots$ für Meta-Variblen.
  • Unter Knoten (nodes) werden die Löcher (holes) und Labels zusammengefasst
  • Meta-Terme sind alle Meta-Variablen und URL-Konstanten.

Nur eine Teilmenge aller Formeln der URL werden zur unterspezifizierten Repräsentation von semantischen Repräsentationen benötigt, nämlich die existentiell abgelschlossenen konjunktiven Formeln, die underspecified semantic representations (USRs) genannt werden:

underspecified semantic representations (USRs)

basic USRs:

allgemeine USRs: 

Zurück zu dem Beispiel:

In der obigen Abbildung wird folgende USR dargestellt:

Die USR besteht aus den existentiell abgeschlossenen Konjunkten:

  • $\exists l_1\exists l_2\exists v_1 (l_1:ALL(v_1,l_2)),\ldots \exists l_7(l_7:LOVE(v_1,v_2))$; jedes dieser Konjunkte beschreibt einen der 7 Ecken des Graphen ohne die $h_0$-Ecke.
  • $l_7\leq h_1, \ldots l_4\leq h_0$; jeder dieser Konjunkte beschreibt eine der gestrichelten Linien im Graphen; dies sind die Dominanzconstraints.

Plugging

Eine USR beschreibt alle semantischen Repräsentationen (SR), die die USR erfüllen. Um aus einer USR die SRs, die sie erfüllen zu ermitteln, muss man den Löchern in der USR Labels zuordnen und anschließend überprüfen, ob die Dominanzconstraints erfüllt sind. Die nennt man Plugging. Ein Plugging ist eine injektive Abbildung von der Menge der Löcher einer USR in die Menge der Labels.

Für das Beispiel gibt es zwei zulässige Pluggings:

Plugging 1

  • $P_1(h_0) = l_1, P_1(h_1) = l_4, P_1(h_2) = l_7$

Plugging 2

  • $P_2(h_0) = l_4, P_2(h_1) = l_7, P_2(h_2) = l_1$
  • Welche Lesarten werden mit diesen Pluggings repräsentiert?
  • Warum sind andere Pluggings nicht möglich?

Implementing Hole Semantics

Example USR in Prolog notation:

  • USRs are made with lambdas, for example:

$\lambda v. \lambda h. \lambda l. (l:BOXER(v) \wedge l \leq h)$

Semantic Macros (semLexHole.pl)

semLex(noun,M):-
   M = [symbol:Sym,
        sem:lam(X,lam(H,lam(L,and(pred1(L,Sym,X),leq(L,H)))))].

semLex(det,M):-
   M = [type:wh,
        sem:lam(N,lam(V,lam(H,lam(L,some(H1,some(L1,some(L2,some(X,and(hole(H1),
                and(label(L1),and(label(L2),and(que(L2,X,L1,H1),and(leq(L,H1),
                    and(leq(L2,H),and(app(app(app(N,X),H),L1),
                        app(app(app(V,X),H),L))))))))))))))))].
semLex(tv,M):-
   M = [symbol:Sym,
        sem:lam(Z,lam(X,app(Z,lam(Y,lam(H,lam(L,and(pred2(L,Sym,X,Y),leq(L,H))))))))].

semLex(av,M):-
   M = [pol:neg, 
        sem:lam(V,lam(X,lam(H,lam(L,some(S,some(N,and(hole(S),and(label(N),and(not(N,S), and(leq(N,H),and(leq(L,S),app(app(app(V,X),H),L))))))))))))];

   M = [pol:pos,
        sem:lam(V,lam(X,lam(H,lam(L,app(app(app(V,X),H),L)))))].

Semantic Rules (semRulesHole.pl)

combine(t:U,[s:S]):- 
   betaConvert(some(T,and(hole(T),some(L,and(label(L),app(app(S,T),L))))),U).

The Plugging ALgorithm (pluggingAlgorithm.pl)

/*========================================================================
     Declaration of dynamic predicates
========================================================================*/

:- dynamic plug/2, leq/2, hole/1, label/1.
:- dynamic some/3, all/3, que/4.
:- dynamic not/2, or/3, imp/3, and/3.
:- dynamic pred1/3, pred2/4, eq/3.


/*========================================================================
   Main Plugging Predicate (all pluggings)
========================================================================*/

plugUSR(USR,Sem):-
   numbervars(USR,0,_),          % 1 Skolemise USR
   initUSR, 
   assertUSR(USR),               % 2 Break down and assert USR
   top(Top),  
   findall(H,hole(H),Holes),
   findall(L,
           (label(L),\+ parent(_,L)),
           Labels),
   plugHoles(Holes,Labels,[]),   % 3 Calculate a plugging
   url2srl(Top,Sem).             % 4 Construct SRL formula


/*========================================================================
   Asserting immediate dominance relations to the Prolog database
========================================================================*/

parent(A,B):- imp(A,B,_).
parent(A,B):- imp(A,_,B).
parent(A,B):- or(A,B,_).
parent(A,B):- or(A,_,B).
parent(A,B):- and(A,B,_).
parent(A,B):- and(A,_,B).
parent(A,B):- not(A,B).
parent(A,B):- all(A,_,B).
parent(A,B):- some(A,_,B).
parent(A,B):- que(A,_,B,_).
parent(A,B):- que(A,_,_,B).
parent(A,B):- plug(A,B).


/*========================================================================
   Transitive Closure of Dominance
========================================================================*/

dom(X,Y):- dom([],X,Y).

dom(L,X,Y):- 
   parent(X,Y), 
   \+ memberList(parent(X,Y),L).

dom(L,X,Y):- 
   leq(Y,X), 
   \+ memberList(leq(Y,X),L).

dom(L,X,Z):- 
   parent(X,Y), 
   \+ memberList(parent(X,Y),L),
   dom([parent(X,Y)|L],Y,Z).

dom(L,X,Z):- 
   leq(Y,X), 
   \+ memberList(leq(Y,X),L),
   dom([leq(Y,X)|L],Y,Z).


/*========================================================================
   Plugging Holes with Labels
========================================================================*/

plugHoles([],_,Plugs):-
   admissiblePlugging(Plugs).

plugHoles([H|Holes],Labels1,Plugs):-
   admissiblePlugging(Plugs),
   selectFromList(L,Labels1,Labels2),
   plugHoles(Holes,Labels2,[plug(H,L)|Plugs]).


/*========================================================================
   Check whether plugging is propers
========================================================================*/

admissiblePlugging(Plugs):-
   retractall(plug(_,_)), 
   findall(X,(memberList(X,Plugs),assert(X)),_),
   \+ dom(A,A),
   \+ ( parent(A,B), parent(A,C), \+ B=C, dom(B,D), dom(C,D)).


/*========================================================================
    Top of a USR
========================================================================*/

top(X):- dom(X,_), \+ dom(_,X), !.


/*========================================================================
   From USRs to FOLs
========================================================================*/

url2srl(H,F):-
   hole(H),
   plug(H,L),
   url2srl(L,F).

url2srl(L,all(X,F)):-
   all(L,X,H),
   url2srl(H,F).

url2srl(L,some(X,F)):-
   some(L,X,H),
   url2srl(H,F).

url2srl(L,que(X,F1,F2)):-
   que(L,X,H1,H2),
   url2srl(H1,F1),
   url2srl(H2,F2).

url2srl(L,imp(F1,F2)):-
   imp(L,H1,H2),
   url2srl(H1,F1),
   url2srl(H2,F2).

url2srl(L,and(F1,F2)):-
   and(L,H1,H2),
   url2srl(H1,F1),
   url2srl(H2,F2).

url2srl(L,or(F1,F2)):-
   or(L,H1,H2),
   url2srl(H1,F1),
   url2srl(H2,F2).

url2srl(L,not(F)):-
   not(L,H),
   url2srl(H,F).

url2srl(L,eq(X,Y)):-
   eq(L,X,Y).

url2srl(L,F):-
   pred1(L,Symbol,Arg),
   compose(F,Symbol,[Arg]).

url2srl(L,F):-
   pred2(L,Symbol,Arg1,Arg2),
   compose(F,Symbol,[Arg1,Arg2]).


/*========================================================================
   Assert USR to Prolog database
========================================================================*/

assertUSR(some(_,F)):-   
    assertUSR(F).

assertUSR(and(F1,F2)):-
    assertUSR(F1),
    assertUSR(F2).

assertUSR(F):- 
    \+ F=and(_,_),
    \+ F=some(_,_),
    assert(F).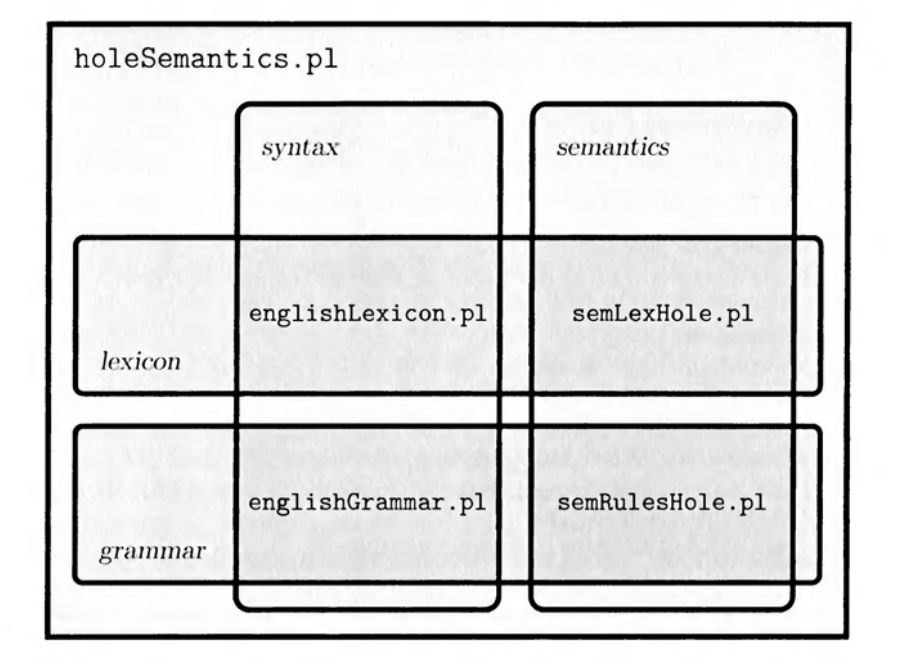

Übung

  • Schaue dir den Output von holeSemanticsTestSuite an. Werden alle Lesarten produziert? Werden nur die richtigen Lesarten produziert?
  • Implementiere die ditransitiven Verben in Hole Semantics.

Warnung:

Die Umsetzung der Negation ist nicht gut, es kommt zu falschen Ergebnissen.

Beispiele:

####################################
Keller Storage:
Sentence: [mia,does,not,dance,and,smoke] (2 readings)
1 ~ (dance(mia) & smoke(mia))

Sentence: [mia,does,not,dance,and,does,smoke] (1 readings)
1 (~ dance(mia) & smoke(mia))

Sentence: [mia,does,dance,and,does,not,smoke] (1 readings)
1 (dance(mia) & ~ smoke(mia))

####################################
Hole Semantics:
Sentence: [mia,does,not,dance,and,smoke] (2 readings)
1 ~ (dance(mia) & smoke(mia))

Sentence: [mia,does,not,dance,and,does,smoke] (1 readings)
1 ~ (dance(mia) & smoke(mia))

Sentence: [mia,does,dance,and,does,not,smoke] (1 readings)
1 ~ (dance(mia) & smoke(mia))

Kapitelnavigation:

    Noch keine Kommentare eingereicht. Bitte hilf uns diese Aufgabe zu verbessern.

    Schreibe einen Kommentar

    Deine personenbezogenen Daten werden nicht gespeichert!