Chapter 2: Lambda Calculus

Wie kann der Prozess der Zuweisung von semantischen Repräsentationen (z.B. in Form von prädikatenlogischen Formeln) zu natürlichsprachlichen Ausdrücken automatisiert werden?

Compositionality (BB: 2.1)

Gegeben einen natürlichsprachlichen Satz (z.B. “Vincent likes Mia”), gibt es einen systematischen Weg seine semantische Repräsentation zu konstruieren?

Wie können wir garantieren, dass “Vincent likes Mia” und “Mia likes Vincent” zwei verschiedene semantische Repräsentationen zugewiesen bekommen?

Lösungsidee: Die Wörter liefern Teile der semantischen Repräsentation (“MIA”, “LOVE(X,Y)”) und die Syntax steuert ihre Verklebung (“LOVE(VINCENT,MIA)”).

Syntax: Syntaktische Analysen sollten hierarchisch sein = Sätze sollten zerlegt werden in Teile und Unterteile usw.

Semantische Komposition ≈ Verkleben der Teile

Lexicon entries look approximately like this: LOVE(?,?), MIA, VINCENT.

Syntactic analysis of a sentence is a tree whose non-leaf nodes represent complex syntactic categories and whose leaves represent lexical items.

Two Experiments (BB: 2.2)

Experiment 1

Experiment 2

Die Probleme des 1. Experiments waren,

• dass wir je zwei Regeln für die Konstituenten benötigt haben (für das Quantoren-freie Fragment und das Fragment mit den quantifizierten NPs)
• dass wir uns auf arg/3 für die Verklebung der Information verlassen haben.
  

Lösungsidee: Wir machen die fehlende Information der Konstitutenten explizit und weisen ihnen eigene Parameter zu.

Beispiele:

• Der semantischen Repräsentation eines Nomens wie woman fehlt die Information, über welches Objekt die Eigenschaft woman prädiziert:

noun(X,woman(X))--> [woman].

• Der semantischen Repräsentation intransitiver Verben fehlt die Information über ein Argument und der von transitiven Verben die von zwei Argumenten:

iv(Y,snort(Y))--> [snorts].
tv(Y,Z,like(Y,Z))--> [likes].

• Die semantische Repräsentation eines Artikel wie a basiert auf einer quantifizierten Formel, der drei Informationen fehlen, nämlich
  (1) die Variable über die quantifiziert wird,
  (2) die Restriktion, die vom Nomen geliefert werden wird und
  (3) der nukleare Skopus, der vom Verb geliefert werden wird:

det(X,Restr,Scope,some(X,and(Restr,Scope)))--> [a].

• In einer quantifizierten NP liefert das Nomen die Information über die Restriktion, so dass nur noch die Information über den nuklearen Skopus fehlt:

np(X,Scope,Sem)--> det(X,Restr,Scope,Sem), noun(X,Restr).

• Einer VP fehlt nur noch die Information über das Subjekt:

vp(X,Sem)--> iv(X,Sem).
vp(X,Sem)--> tv(X,Y,SemTV), np(Y,SemTV,Sem).

• Einem Satz fehlt schließlich keine Information mehr:

s(Sem)--> np(X,SemVP,Sem), vp(X,SemVP).

• Bleibt nur noch das Problem der Eigennamen, die natürlich keine fehlende Information haben:

pn(mia)--> [mia].

• Zuvor haben wir jedoch eine NP-Regel für quantifizierte NPs mit zwei zusätzlichen Parametern X und Scope angegeben. Für Eigennamen wollen wir jetzt keine NP-Regel mit einer anderen Stelligkeit. Die Lösung ist, die folgende Regel, die bei der weiteren Verklebung zu einem Satz dafür sorgt, dass der Eigenname SemPN zum Argument des Verbs wird und die Semantik des Verbs (oder der VP) zur Semantik der VP (oder des Satzes) wird:

np(SemPN,Sem,Sem)--> pn(SemPN).

The Lambda Calculus (BB: 2.3)

Zur Erinnerung: In Experiment 2 haben wir eine erste Lösung für unsere Aufgabe, automatisch zu einem sprachlichen Ausdruck eine semantische Repräsentation zu produzieren, gefunden.

Lambda-Kalkül

• In diesem Kurs wird das Lambda-Kalkül als eine notationelle Erweiterung der Logik erster Ordnung betrachtet, die es uns erlaubt, Variablen mit Hilfe eines Lambda-Operators zu binden. Durch Lambda gebundene Variablen sind ‚Platzhalter‘ für fehlende Informationen.
• Wenn wir einen Lambda-Ausdruck neben einen anderen Ausdruck (den Argument-Ausdruck) setzen, ist das eine Anweisung, den Platzhalter durch den Argument-Ausdruck zu substituieren. Diese Anweisung wird als funktionale Applikation bezeichnet.
• Die Operation der $\beta$-Konversion führt die eigentliche Arbeit der Substitutionen aus.
• Zusätzlich sorgt die $\alpha$-Konversion für die Buchhaltung der gebundenen Variablen.
• Das Lamba-Kalkül ist eine Art Klebesprache, also eine „Programmiersprache“, die sich einer einzigen Aufgabe widmet: dem Zusammenkleben der Elemente, die zum Aufbau semantischer Repräsentationen benötigt werden.

Der Lamba Operator

Der Lambda Operator markiert fehlende Information, indem die fehlende Information als gebundene Variable repräsentiert wird.

• Beispiel eines simplen Lambda Ausdrucks:
  • $\lambda x.MAN(x)$
  • Das Prefix $\lambda x$ bindet das Vorkommen von $x$ in $MAN(x)$
  • $\lambda x.MAN(x)$ kann gelesen werden als: ‚Ich bin das 1-stellige Prädikat $MAN$ und ich suche einen Term, der meinen Argumentplatz ausfüllt.‘

Funktionale Applikation

Der @-Operator wird zur Kennzeichnung der funktionalen Applikation verwendet. Das heißt, er zeigt an, auf welches Argument (der Ausdruck rechts vom @-Operator) der Funktor (links vom @-Operator) anzuwenden ist.

Beispiel:

$\lambda x.MAN(x)@VINCENT$

• Der Ausdruck $\lambda x.MAN(x)$ wird Funktor genannt. Den Ausdruck $VINCENT$ nennt man Argument.
• Intuitiv heißt das: ersetze alle Vorkommen des Platzhalters $x$ im Funktor durch das Argument $VINCENT$.
  

$\beta$-Konversion

Die eigentliche Substitution wird durch die $\beta$-Konversion durchgeführt.

Aus

$\lambda x.MAN(x)@VINCENT$

entsteht durch $\beta$-Konversion

$MAN(VINCENT)$

Die Variablenbindung $\lambda x.$ am Anfang des Ausdrucks fällt weg und alle Vorkommen von $x$, die durch $\lambda x$ gebunden waren, werden durch das Argument $VINCENT$ ersetzt.

Video: $\beta$-Konversion am Beispiel des Satzes „Vincent loves a boxer“:

Video: $\beta$-Konversion bei doppelter Applikation und Abstraktion

Implementing Lambda Calculus (BB: 2.4)

Was müssen wir tun?

1. entscheiden wie $\lambda x. E$ und $\mathcal{F}@\mathcal{A}$ repräsentiert werden sollen.
2. Implementierung von $\beta$-Konversion
3. Implementierung von $\alpha$-Konversion

Lambda-Abstraktion und Applikation in Prolog

• $\lambda x. E$ repräsentieren wir als lam(X,E).
• $\mathcal{F}@\mathcal{A}$ repräsentieren wir als app(F,A).

Implementing $\beta$-conversion

• Problem: Der semantische Output gibt lediglich an, wie die Information zu verkleben ist, um die semantische Repräsentation des Satzes zu erhalten.
• Ziel: Ausführung aller $\beta$-Konversionen.
• Idee: Stack zur Verwaltung der Argumente.

Expression                                          Stack
app(app(lam(Z,lam(Y,invite(Y,Z))),mia),vincent)        []
app(lam(Z,lam(Y,invite(Y,Z))),mia)              [vincent]
lam(Z,lam(Y,invite(Y,Z)))                  [mia, vincent]
lam(Y,invite(Y,mia))                            [vincent]
invite(vincent,mia)                                    []

Aufgabe: Übertrage die Darstellung von der Präfix- in die Infixnotation und erkläre, wie der Stack eingesetzt wird (was geschieht bei funktionaler Applikation, was bei Abstraktion?).

Das folgende Bild zeigt, die Aufspaltung eines Ausdrucks, der keine funktionale Applikation ist:

Implementierung:

Aufgabe: Bearbeiten Sie die folgenden Aufgaben aus dem Buch:

Grammar Engineering (BB: 2.5)

Unser Ziel ist eine größere Grammatik, die einen größeren Sprachbereicht umfasst.

Die Grammatik sollte

• modular
• erweiterbar
• wiederverwendbar
  sein

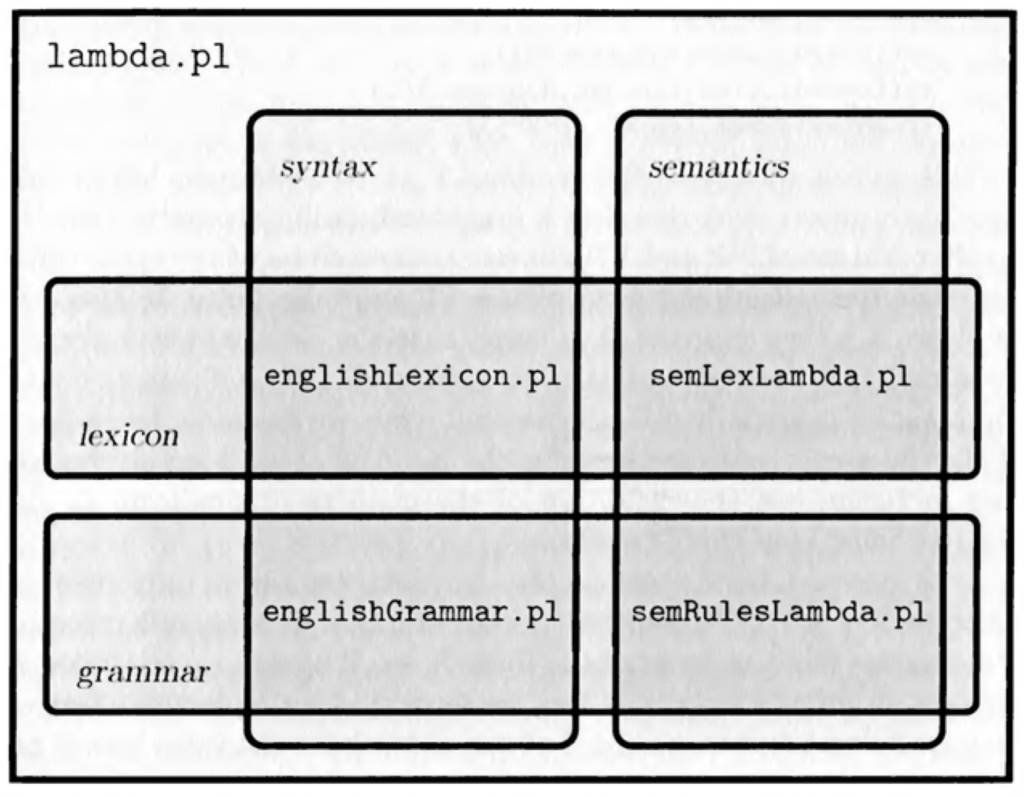
Aufgaben

1. Konsultiere die oben genannten 4 Dateien (EnglishGrammar.pl, semRulesLambda.pl, EnglishLexicon.pl, SemLexLambda.pl) und verfolge den trace von einfachen Anfragen, wie ?- vp(L,[cleans,a,building],[]),member(sem:Sem,L). Benutze s (skip), um uninteressante Zwischenschritte zu überspringen.

2. Konsultiere die Datei lambda.pl und mache dich mit den angebotenen Prädikaten vertraut. Mit ?- info. erhältst du jeder Zeit eine Übersicht.
3. Füge folgendes in die Grammtik ein:
   1. deinen eigenen Namen als Proper Name
   2. das Nomen ‚Pizza‘
   3. das transitive Verb ‚meet‘
4. Bearbeite die folgenden Quizaufgaben

Zusatzaufgaben für Fortgeschrittene

Bearbeite die folgenden Aufgaben aus dem Buch:

Exercise 2.5.1 Find out how copula verbs are handled in the lexicon and grammar, and how the semantic representations for sentences like Mia is a boxer and Mia is not Vincent are generated.

Exercise 2.5.2 Extend the grammar so that it handles expressions of the form Vincent is male, Mia and Vincent are cool, and Marsellus or Butch is big.

Exercise 2.5.3 Extend the grammar so that it handles expressions of the form Vincent and Jules are in a restaurant and Butch is on a motorbike.

Exercise 2.5.4 Add the preposition without to the lexicon, and define a new semantic macro that takes the implicit negation of this preposition into account. For instance, a man without a weapon should receive a representation such as :$\exists X (man(X) \wedge \neg \exists Y (weapon(Y) \wedge with(X,Y)))$.

Exercise 2.5.5 Extend the grammar (the syntax rules and the lexicon) to cover plural forms of nouns. Introduce a new feature in the lexical entries to express number information. Then add entries for determiners and classify
them as combining with singular nouns only (for instance the determiner a), combining with plural nouns only (for instance both, or all), or combining with either (for example the).